長野県公立高校対策問題【数学:問3】
高得点を狙うには外せない!
【問3のⅠ】
お決まりの一次関数の利用の文章問題
表1は、スマホを使っている人のための
「ある電話会社」の電話料金プランです。
図は、1か月の通話時間をx分、そのときの電話料金をy円として、プランBのxとyの関係をグラフに表したものです。
このプランでは、月額基本使用料と通話料金の合計が
1か月の電話料金になります。
ただし、無料通話分の時間内であれば、基本使用料だけが電話料金になります。
あなたは、「スマホ代を少しでも抑えたい」という
友達の冬香さんから相談を受け、どのプランを選ぶべきかを一緒に考えることにしました。
冬香さんに最適なアドバイスをしてあげるため、以下の問いに答えていきましょう。
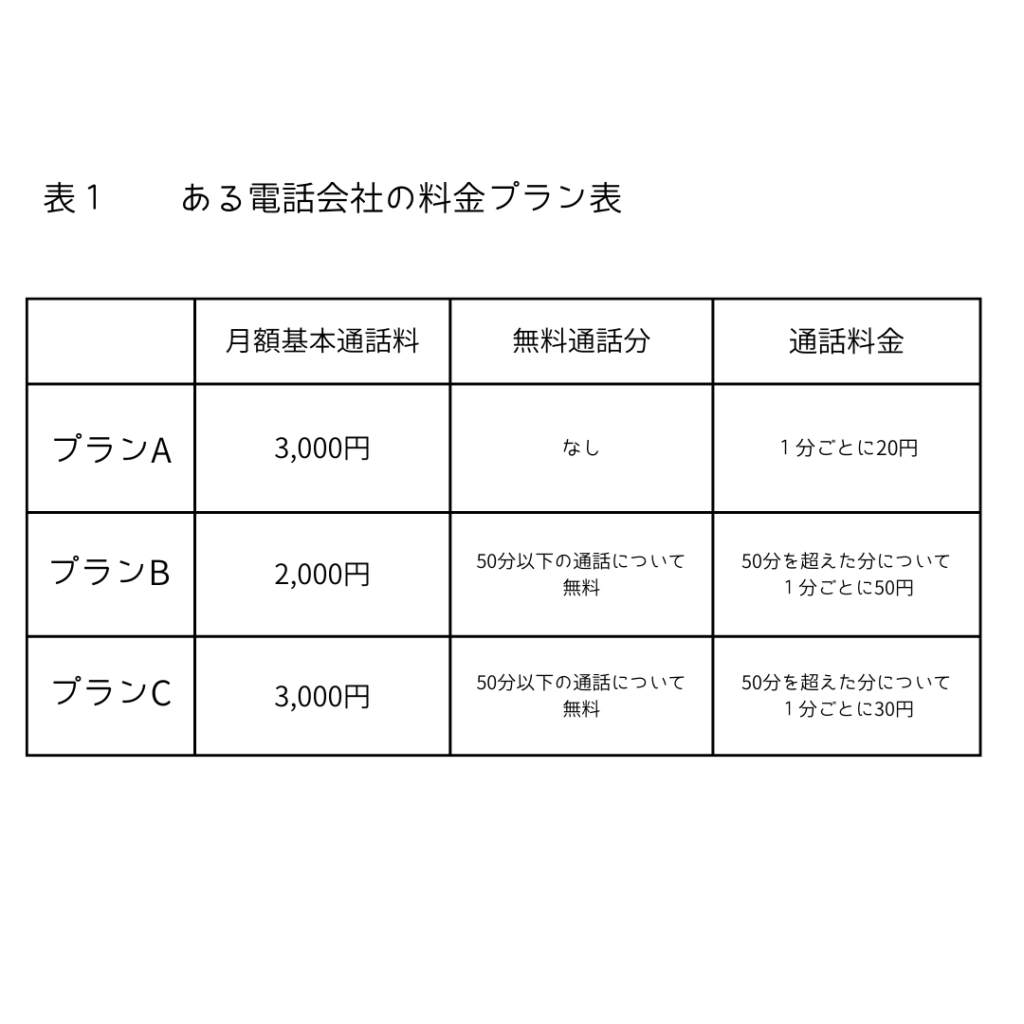
図
(1)プランBで、1か月の通話時間が80分のときの電話料金を求めなさい。
【ポイント】
一次関数の利用は、最初にグラフの縦軸と
横軸のひとメモリがいくつなのか考えよう。
横軸は0~50までに5メモリ。
だから、ひとメモリは10分。
縦軸は0~1000までに2メモリ。
だから、ひとメモリは500円。
これは必ず最初に確認しておくこと!
では、問題にとりかかるよ。
グラフを読めば、計算はしなくてもよいです!
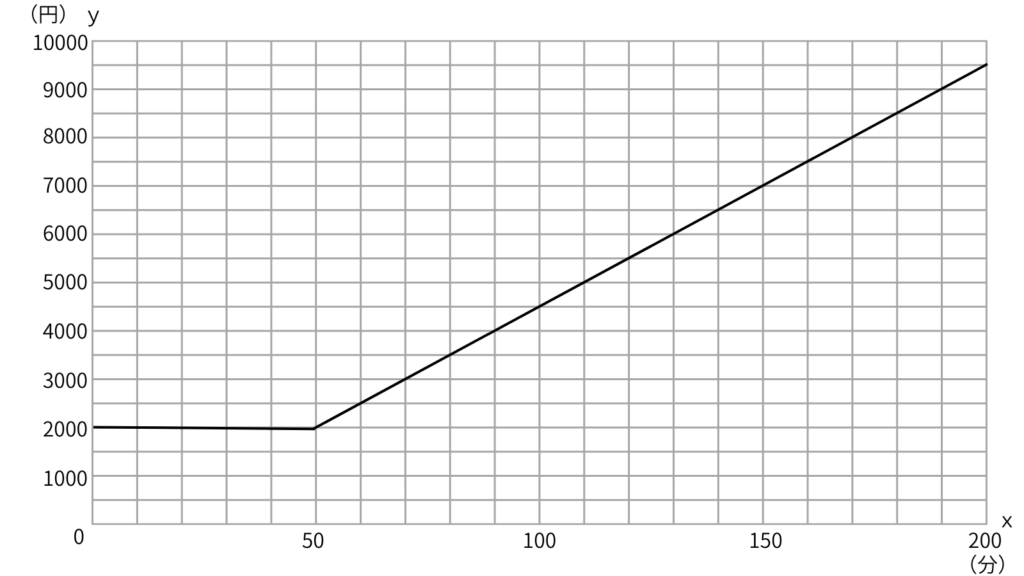
通話時間が80分のときの料金をグラフから見つけよう。
矢印をたどっていけばできるよ。
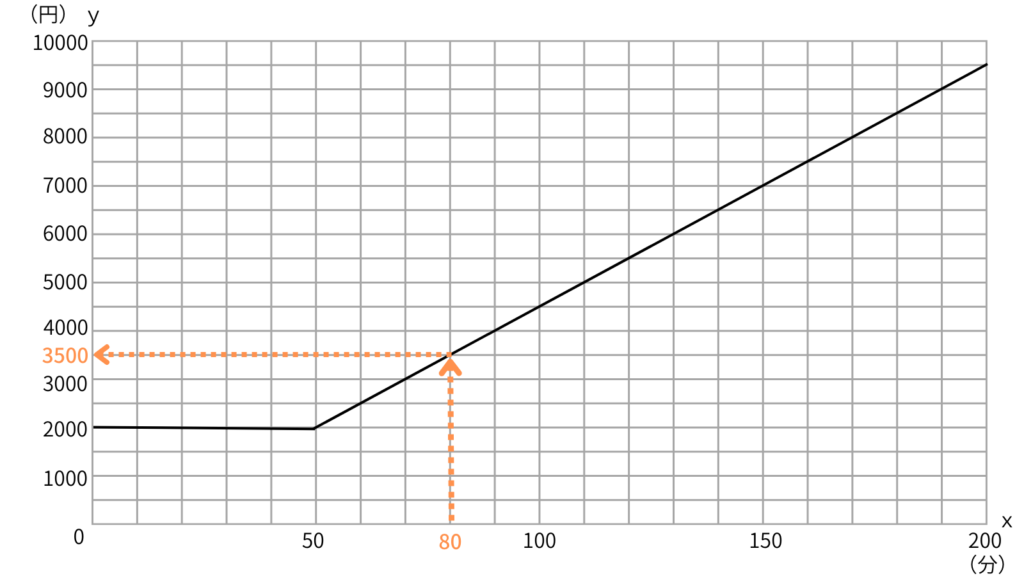
こんな感じ。
80分のときは3500円。
よって
答えは3500円
(2)プランA、プランCのxとyの関係式を表すグラフ(0≦x≦200)を、図に描き入れなさい。
【ポイント】
直線は通る点を2点見つければ、描ける!
傾きが変わる部分を発見しよう!
基本使用料は契約したら必ず発生する料金。
一切使わなくても払う必要のある料金だよ。
まずプランAから。
プランAは基本使用料が3000円。
通話時間が0分でも3000円。
つまり(0,300)の点を通る。
また、通話時間が200分のときの通話料は
20円×200分=4000円。
通話料金は基本使用料と通話量の合計。
だから、4000円+3000円=7000円。
つまり(200,7000)の点を通る。
この2点をぐりぐりして直線でつなげばもう完成!
次にプランC。
プランCは基本使用料は3000円。
無料通話が50分含まれているから50分までは3000円。
つまり(0,3000)と(50,3000)を通る。
ここで、この2点から直線が描ける。
通話時間が50分以上だと通話料金を払う必要がある。
だから、料金の求め方が変わるよ。
200分だと通話料が発生する時間は
200分-50分=150分。
だから、30円×150分=4500円。
そこに基本使用料が入るから
4500円+3000円=7500円。
つまり(200,7500)を通る。
この2点をぐりぐりして直線でつなげばもう完成!
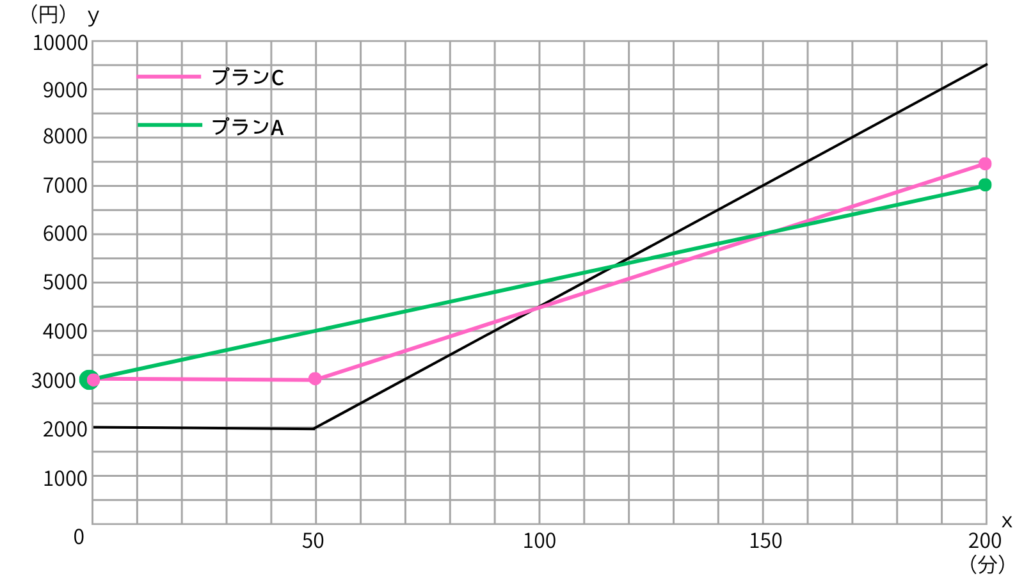
グラフを描くときに、すべての点を取る必要はないよ。
それやってると時間もかかっちゃうしね。
通る点を2点だけ求めるだけでOK!
問題もエコで解いていきましょう。
(3)通話時間が130分のとき、どのプランの電話料金が最も安いかは、電話料金を計算しなくてもグラフから判断できます。
どのプランが一番安いですか。
また、そう判断した理由を説明しなさい。
【ポイント】
グラフが描ければ、わかることはたくさんある!
前の問題で描いたグラフに【通話時間が130分】のところに線を入れてみよう。
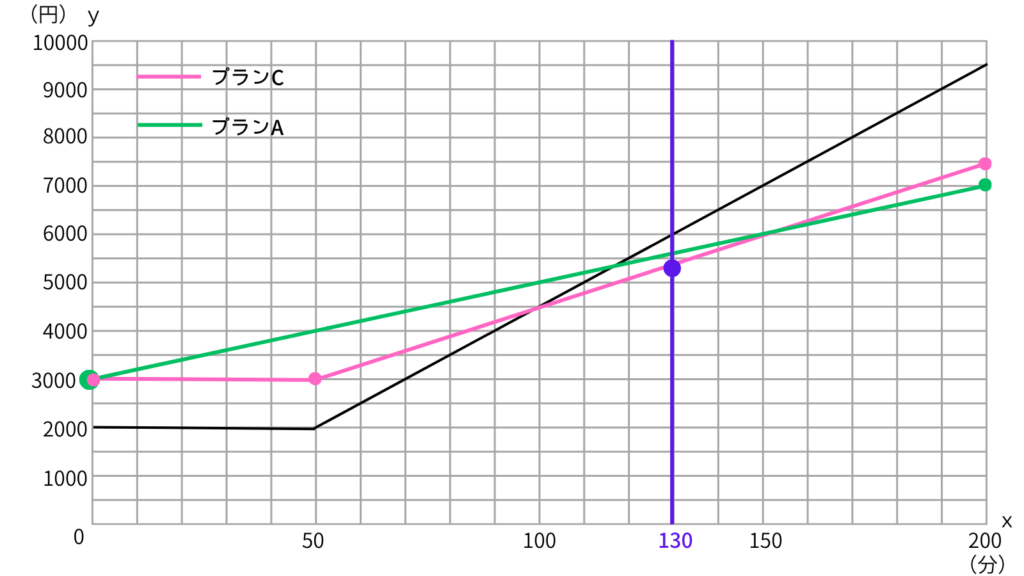
するとyが小さいところ(青●の部分)が
一番安いってわかるよ。
なので、プランCが一番安いって判断できる。
これって計算はなんにもしてないよね。
ただ、グラフ見てるだけ。
これを答えにすべくまとめると
プランCが一番安い。
xが130のときのyの値をグラフから比べる。
となるよ。
(4)冬香さんは、この電話会社とプランBで契約しています。
今までは、通話時間が平均して80分でしたが、来月より学校の課題でグループワークをするため、メンバーとの連絡が増える予定です。
今のプランBのまま変更せずに電話料金をほかのプランより安く抑えるには1ヶ月あたり何分までに抑えれば 良いかを一緒に考えました。
プランBのグラフが他のプランよりも
安くなっている通話時間はプランCとの境目に
あたる( ㋐ )分以内に抑えれば良さそうだね。
「でもこの通話時間だと足りない…」
そう思った冬香さんとあなたは、
「長い時間、通話しても安くなるプランにしたい!」と思って、通話時間を200分にした場合を考えました。
通話時間が200分のときは、プラン( ㋑ )のグラフが他のプランよりも安くなっている。
だから、プラン( ㋑ )が良さそうだね。
㋐にあてはまる値、㋑にあてはまるアルファベットを答えなさい。
【ポイント】
これもグラフから考えることができるよ。
関数の利用の問題はグラフでとける問題がたくさんあるよ。
しっかりグラフをかけるようにしておこう!
はい、じゃグラフを見てみよう。
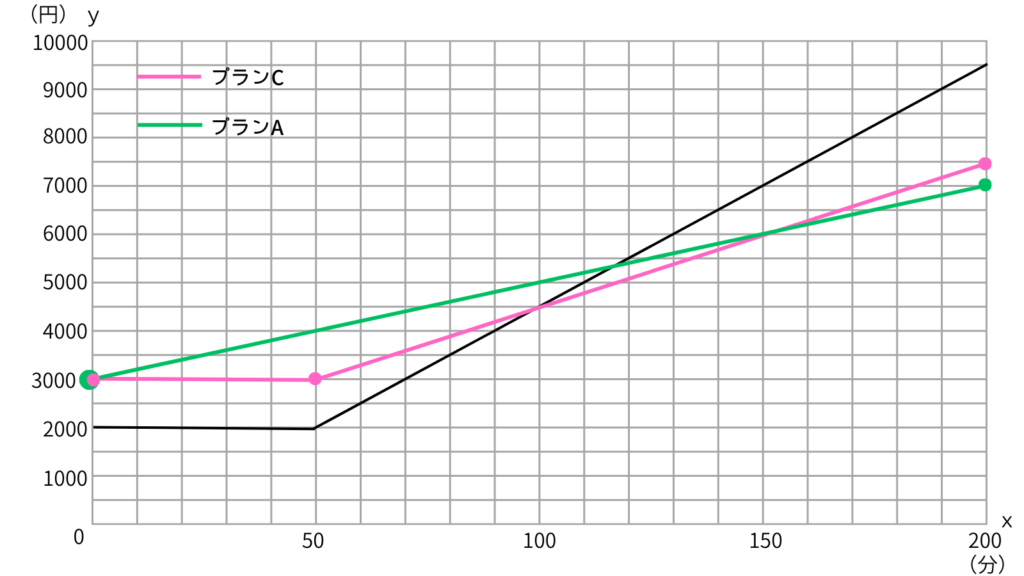
プランBが一番安いのはプランCと交わるところまで。
つまり100分までは、プランBがほかのどのプランよりも安いって判断できる。
つまり㋐の答えは100になる。
次は、200分の場合を考える。
これもグラフからプランAが一番安いって判断ができる。
よって㋑の答えはAになる。
(5)では、実際に通話時間が190分になるとしたとき、
今のプランBをプラン( ㋑ )に変更したときの
1か月当たりの電話料金がいくら安くなるかを求めなさい。
【ポイント】
グラフから絞り込む。
そして、細かい数字は計算で求める!
これは、関数の利用問題のお約束!
まず、問題にはプランBを変更するって書いてあるからプランBは必要だよね。
また、(4)から比較するのはプランAだってことになる。
なので、グラフをプランAとプランBだけにして見やすくしてみよう。
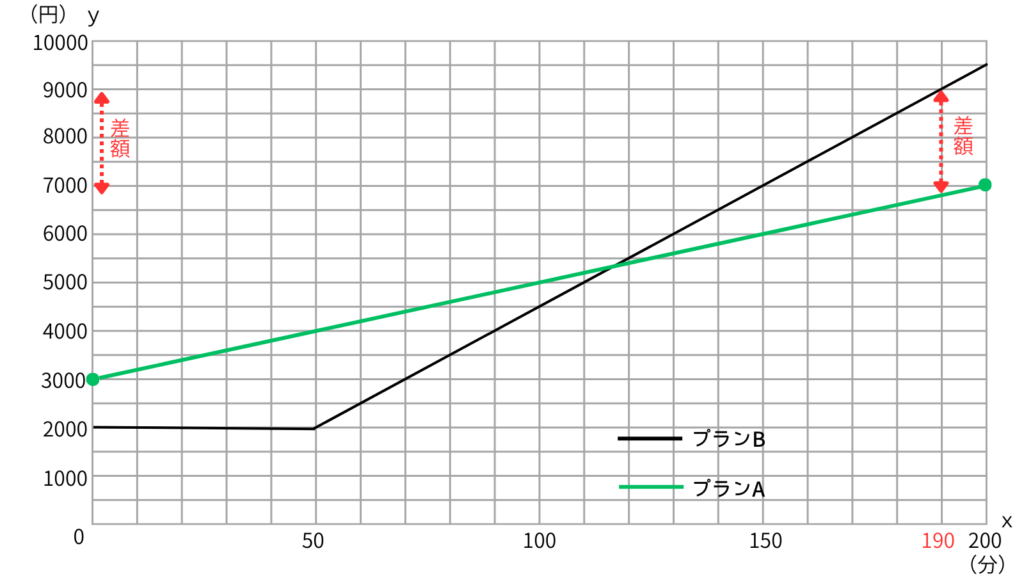
こうしてみると赤の矢印で示した部分が通話時間が190分のときのプランAとプランBの差額だってわかる。
グラフからは、通話時間が190分だとプランBは9000円って読み取れるけど、プランAは6800円くらいかな…。
ただ、数学で〇〇くらいで答えを出すのはよくない。
だから、ここは時間はかかるけど計算しよう!
さっき、見当をつけたものと計算の答えがほぼ一致してくればOK!
直線(一次関数)の式になるので、\[y=ax+b\] になるね。
通話料金とか電気料金とかの表し方は問題に書いてくれてあること多いけど
\[電話料金=基本料金+1分間の通話料金\]で表すことができるよ。
プランAは割と簡単!
基本料金が3000円で1分間の通話料金が20円。
通話時間は \(x\)分 で電話料金が \(y\)円 なので\[y=3000+20x\]
位置を変えてちょっと見やすくして\[y=20x+3000\]これでOK。
次はプランB。基本的には一緒。
基本料金が2000円で1分間の通話料金が50円。
通話時間は \(x\)分 で電話料金が \(y\)円 でと…
でもこれだと間違えてしまうよ。
無料通話が50分あるから料金がかかるのは50分を超えた分。
例えば、通話を140分したら料金を払うのは\(140-50=90\)で90分。
だから、通話時間は \((x-50)\)分 。
これで式をつくると\[y=2000+50(x-50)\]で計算して\[y=2000+50x-2500\]よって\[y=50x-500\]だね。
これで両方のプランで通話料金が計算できるようになるよ。
通話時間が190分のときの電話料金だから \(x=190\) のときを考えよう。
まずはプランAから\[y=20×190+3000\]\[y=3800+3000\]\[y=6800\]
次にプランB\[y=50×190-500\]\[y=9500-500\]\[y=9000\]
よって電話料金の差は\[9000-6800=2200\]
答えは2200円安くなる。
今回はグラフの見た目からの見立てと実際の計算結果が同じだったね。
ただ、こうなることはほとんどない。
つまり、しっかり式を出して計算できるようにしておこう。
ここに一次関数の式の式の求め方を簡単にまとめてあります。
これが分かっていれば、ほぼ問題は解けるはず!
だからグラフと関数の式の出し方は確実にできるようにしておくこと!
【問3のⅡ】
グラフの図形問題(関数の融合)
【ポイント】
グラフの問題は関数の式⇔座標のやりとりがしっかりできればそんなに怖くない!
ただし、原点Oから点\((1,0)\)までの距離、および原点Oから点\((0,1)\)までの距離を1cmとする。
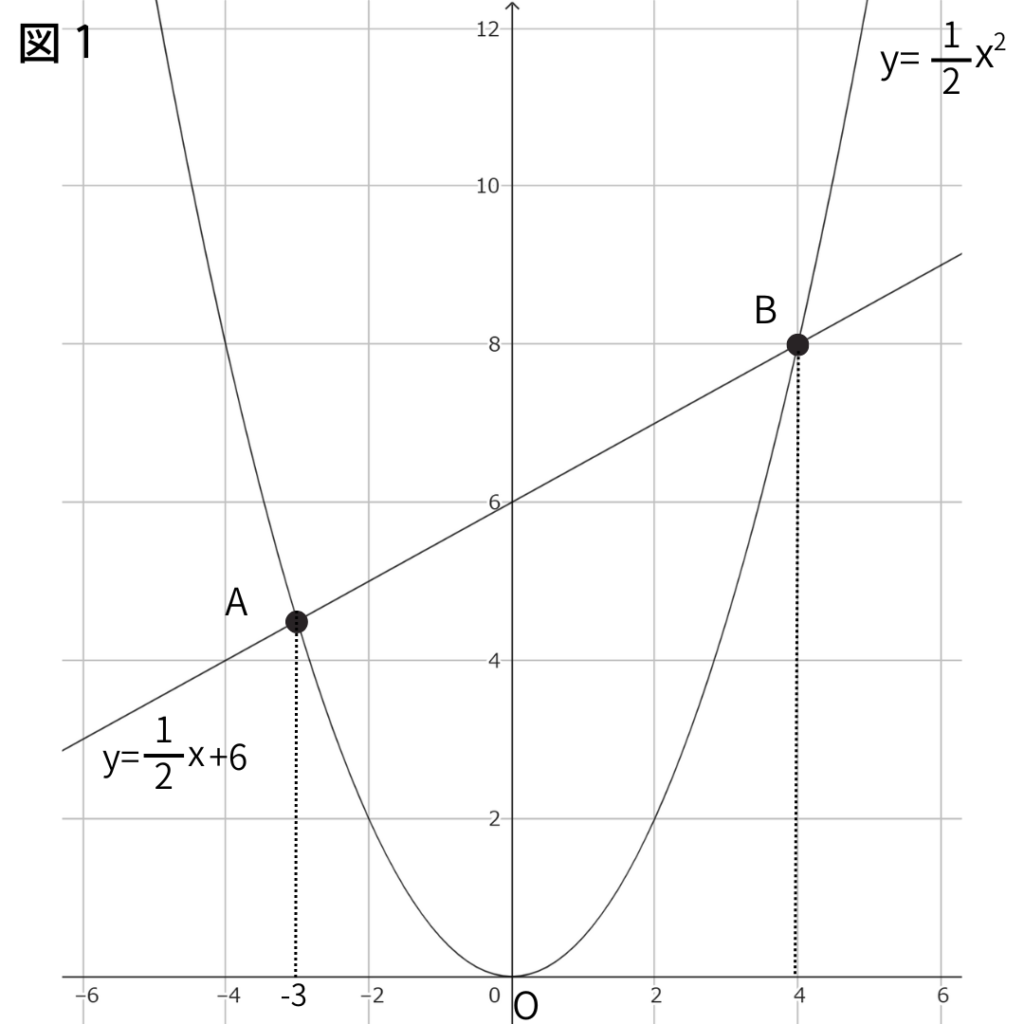
(1)線分ABの長さを求めなさい。
【ポイント】
線分の長さってコトバには三平方の定理で対応!
【三平方の定理とは?】
直角三角形の斜辺と他の2辺の長さの間の関係のこと。
他の2辺の2乗(平方)の和は斜辺の2乗(平方)に等しい。
三(つの辺を)平方(したとき)の定理ってことだと思う…。
関係式は図を見てみてね。
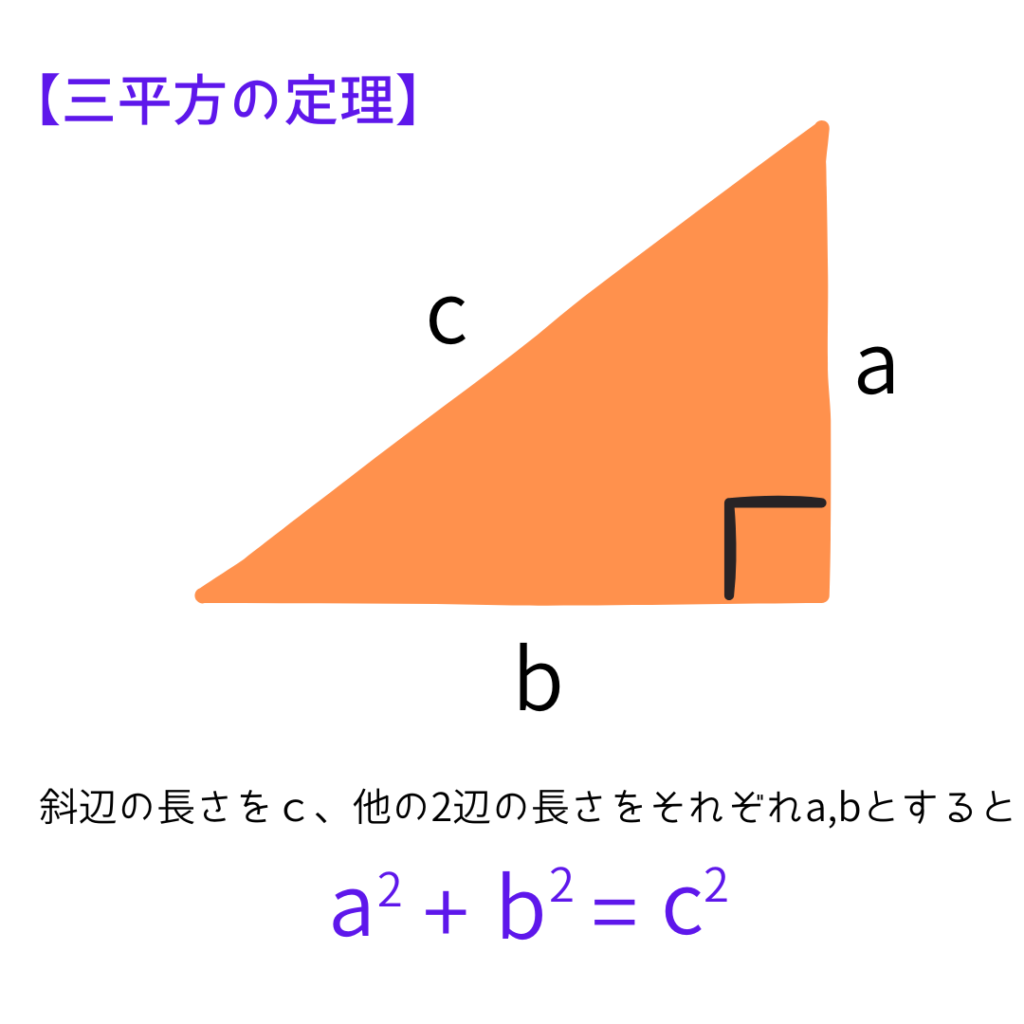
斜めの線分の長さを求めるには、その辺を斜辺にした直角三角形を自分で作ってみよう!
この問題だと、線分ABを斜辺とした直角三角形ABCを作ってみるとこんな感じ。
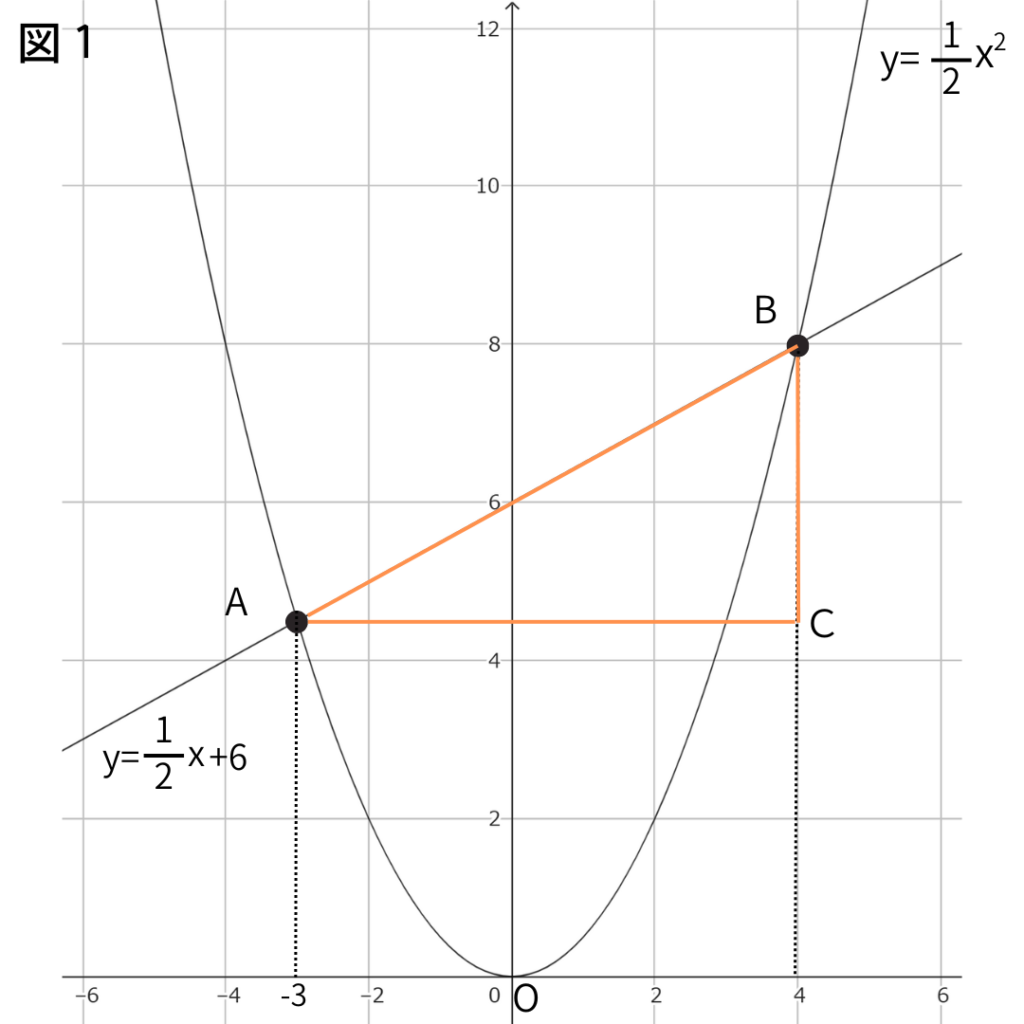
ここで、線分ACと線分BCの長さがわかれば、線分ABの長さがわかるってわけ。
点A・点B・点Cそれぞれの座標から線分の長さが出せる。
つまり座標を求めないといけないね。
点Aは \(y=\frac{1}{2}x^2\) 上にあるので
\(x=3\)を代入して\[y=\frac{1}{2}×3^2\]
\[y=\dfrac{1}{2}×9\]
\[y=\dfrac{9}{2}\]
よって、\(A(-3,\dfrac{9}{2})\)
次は、点B。
点Bも \(y=\frac{1}{2}x^2\) 上にあるので
\(x=4\)を代入して\[y=\frac{1}{2}×4^2\]
\[y=\dfrac{1}{2}×16\]
\[y=8\]
よって、\(B(4,8)\)
Bはグラフから読み取ってもOK!
最後に点C。
点Cは\(x\)座標が点Bと同じで\(y\)座標が点Cと同じだから
よって、\(C(4,\dfrac{9}{2})\)
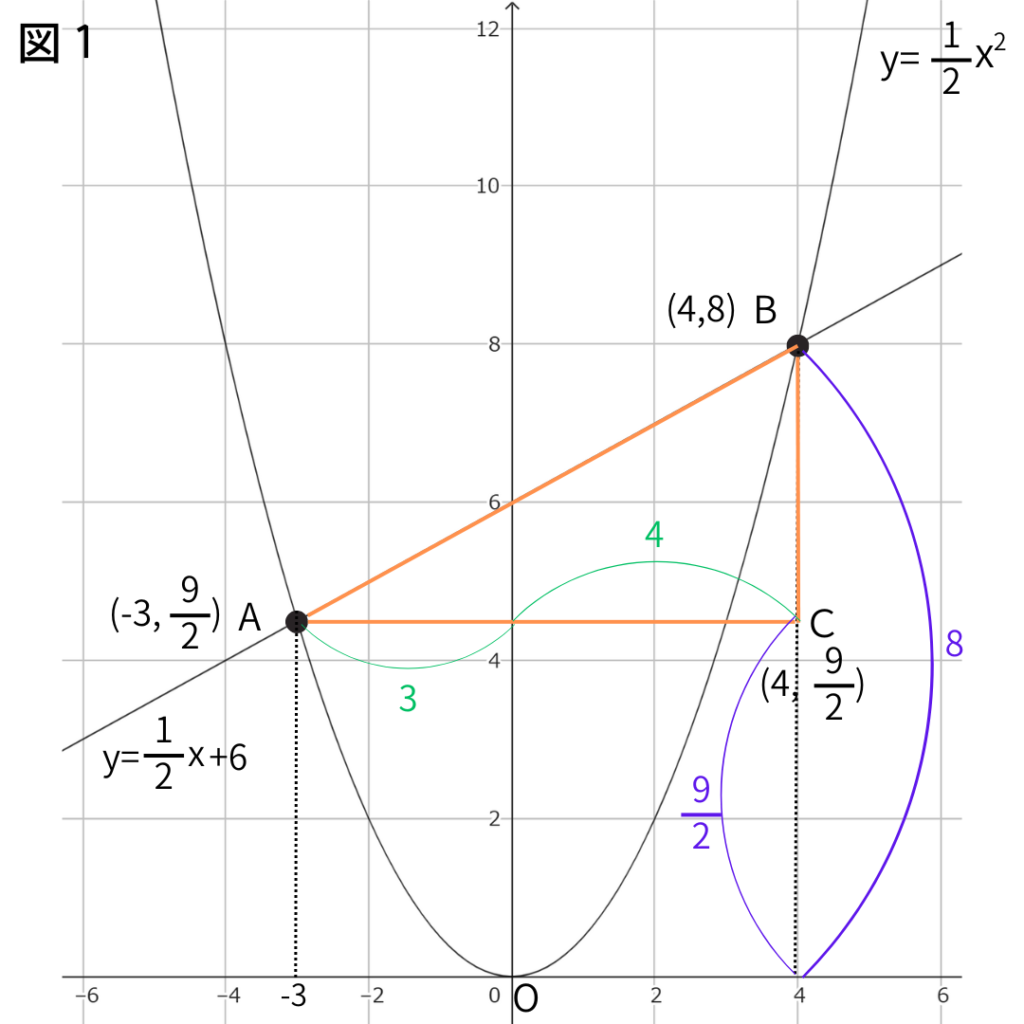
直線ACはみどりの長さのたし算なので、\(7cm\)。
直線BCは青の長さのひき算なので、\(8-\dfrac{9}{2}=\dfrac{7}{2}cm\)。
はい。ではここから三平方の定理の出番。
\(AC^2+BC^2=AB^2\)なので、\[7^2+(\dfrac{7}{2})^2=AB^2\]
見やすくして\[AB^2=7^2+(\dfrac{7}{2})^2\]
あとは計算!\[AB^2=49+\dfrac{49}{4}=\dfrac{245}{4}\]
\[AB=±\sqrt{\dfrac{245}{4}}\]
\[AB=±\dfrac{\sqrt{245}}{\sqrt{4}}\]
\(245=5×7^2、4=2^2\)だから\[AB=±\dfrac{7\sqrt{5}}{2}\]
線分ABはマイナスになることがないので\[AB=\dfrac{7\sqrt{5}}{2}cm\]
(2)図1において、原点Oと点A、点Bを結んでできる△OABの面積を求めなさい。
【ポイント】
関数の図形問題の三角形は2つに分けて考える!
多くの場合はy軸で2つに分けるといいよ!
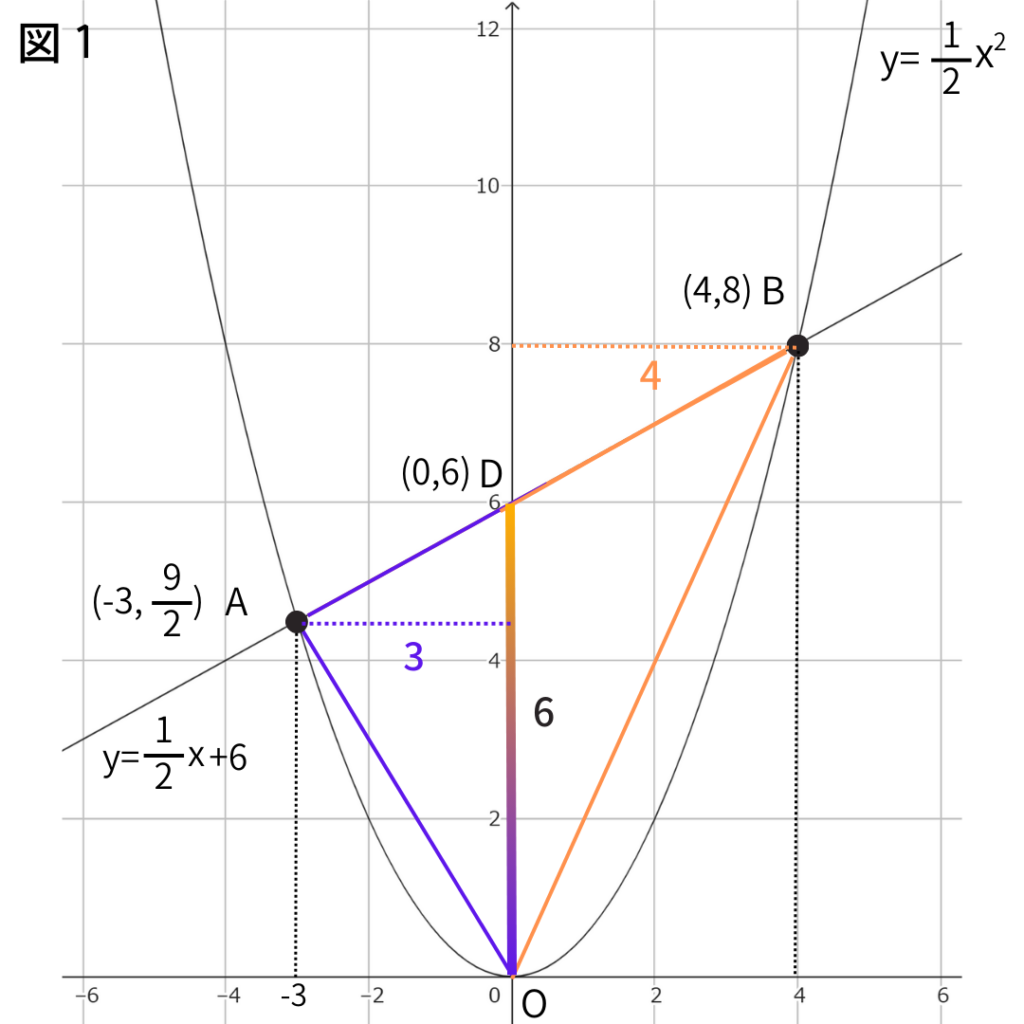
まずは直線lとy軸との交点をDとする。
Dの座標は(0,6)。←切片だから
すると
△OABは△AODと△BODに分けられる。
これで両方の三角形の底辺(OD)と高さが分かる状況になるよ。
(点線の部分がそれぞれの高さです)
△BOD=\(\dfrac{1}{2}×6×4=12㎠\)
△OAB=△AOD+△BODだから\[△OAB=9+12=21\]
よって、答えは21㎠。
(3)図1において、原点Oと点A,点Bを結んでできる△OABの面積を2等分する原点Oを通る直線の方程式を求めなさい。
【ポイント】
三角形の面積を2等分するとき、どこか一つの頂点を通るならその対辺の中点を通れば面積は2等分される!
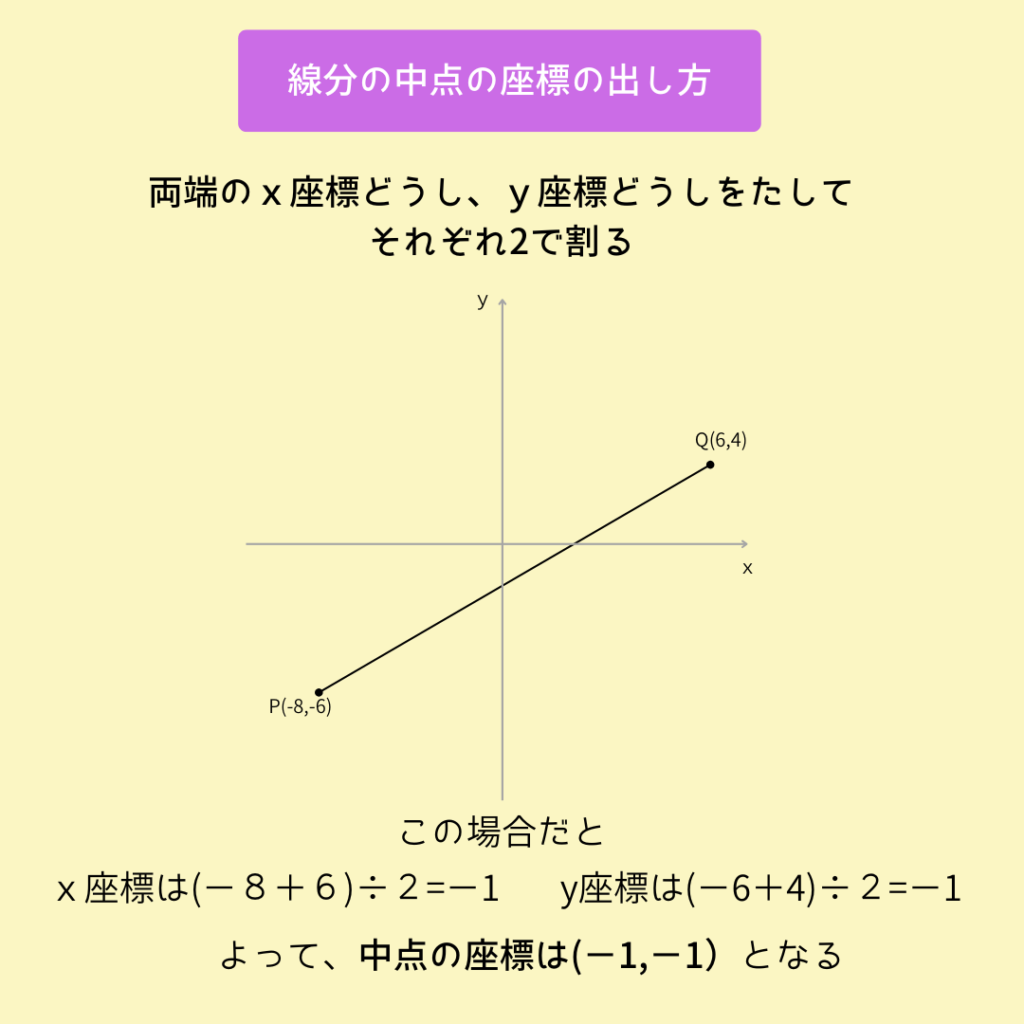
線分の中点の座標の求め方はこれですべてできる。
よく公式みたいになってる。
こんな感じ。
\[M(\dfrac{x\tiny{1}+x\tiny{2}}{2},\dfrac{y\tiny{1}+y\tiny{2}}{2})\]
で求められるよ。
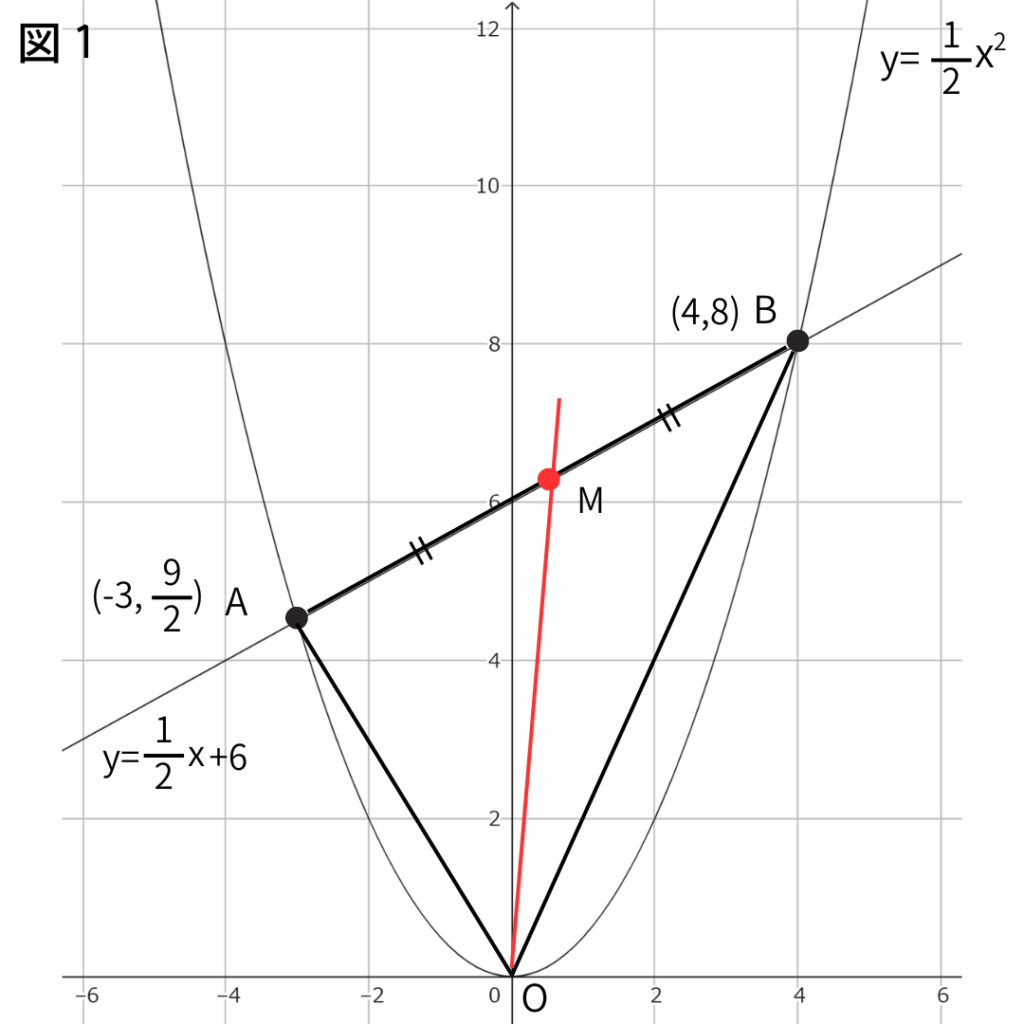
図で表すと面積を2等分する赤色の直線が描ける。
まずは中点を通らないと2等分にならないので、中点の座標を出そう。これはさっきの知識を使ってみよう。
座標は図に入ってるから\[M(\dfrac{(-3)+4}{2},\dfrac{\frac{9}{2}+8}{2})\]だね。
\(x\)座標はそのままでいけそう。
ただ、\(y\)座標は見たことないかたち…
これを分数ではなくすると\[M(\dfrac{(-3)+4}{2},(\frac{9}{2}+8)÷2)\]
あとは計算!\[M(\dfrac{1}{2},\dfrac{25}{4})\]
これで中点の座標はOK。
あとは直線の式だけど候補は2つ。
\[y=ax もしくは y=ax+b\]
よく見ると原点を通ってるから比例。
つまり式は\(y=ax\)に決定!
ここに中点Mの座標を入れると\(a\)が求められる。
また、計算!\[\dfrac{25}{4}=a×\dfrac{1}{2}\]
見やすくして\[\dfrac{1}{2}a=\dfrac{25}{4}\]
分数やだから両辺を2倍\[\dfrac{1}{2}a×2=\dfrac{25}{4}×2\]
\[a=\dfrac{25}{2}\]
だから直線の式は\[y=\dfrac{25}{2}x\]
(4)次の図2において、図1の放物線上を点Aから点Bまでを動く動点Pがある。
動点Pを通り、y軸に平行な直線mと直線ℓとの交点をQとする。
線分PQの長さが3㎝になるような点Pの座標をすべて求めなさい。
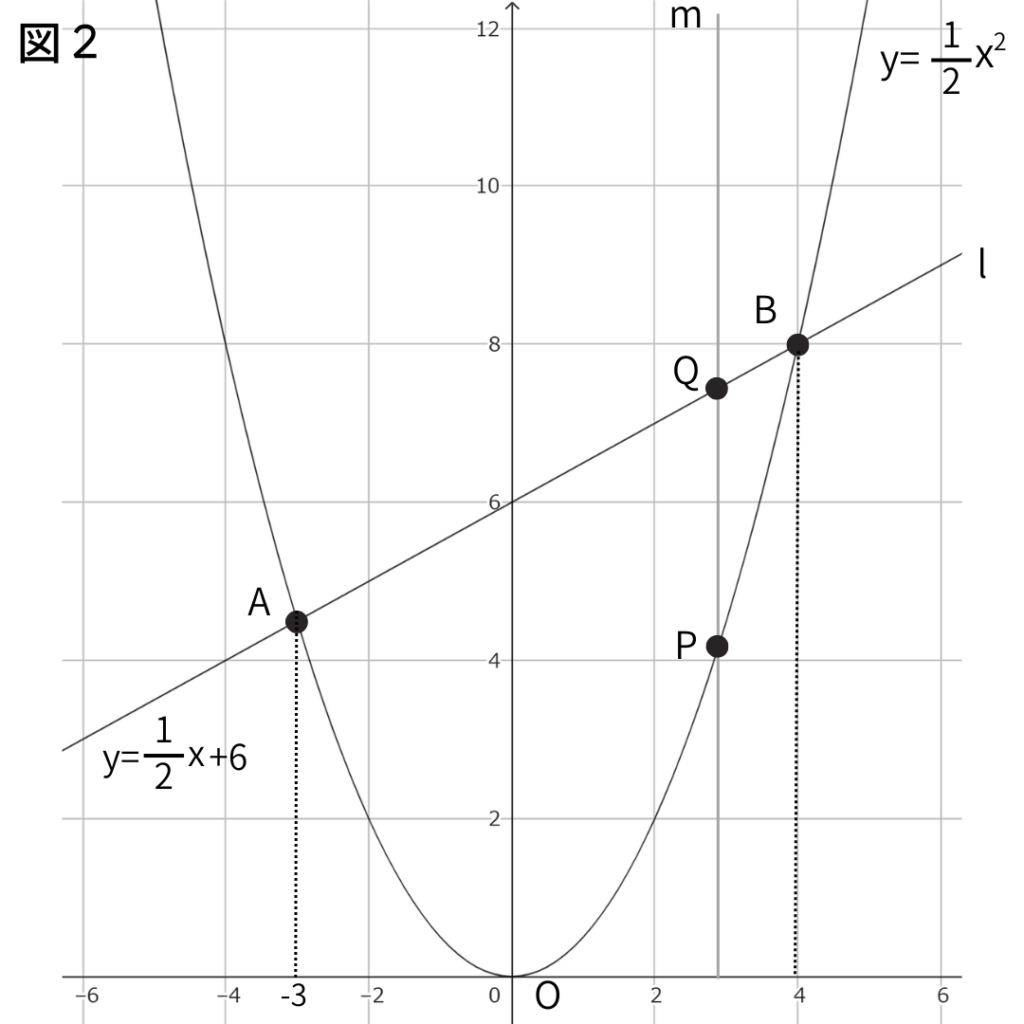
【ポイント】
動点の問題は座標が分からないのでx座標をtとおいて計算していく。
文字を文字で置くから違和感あるけどこれでOK!
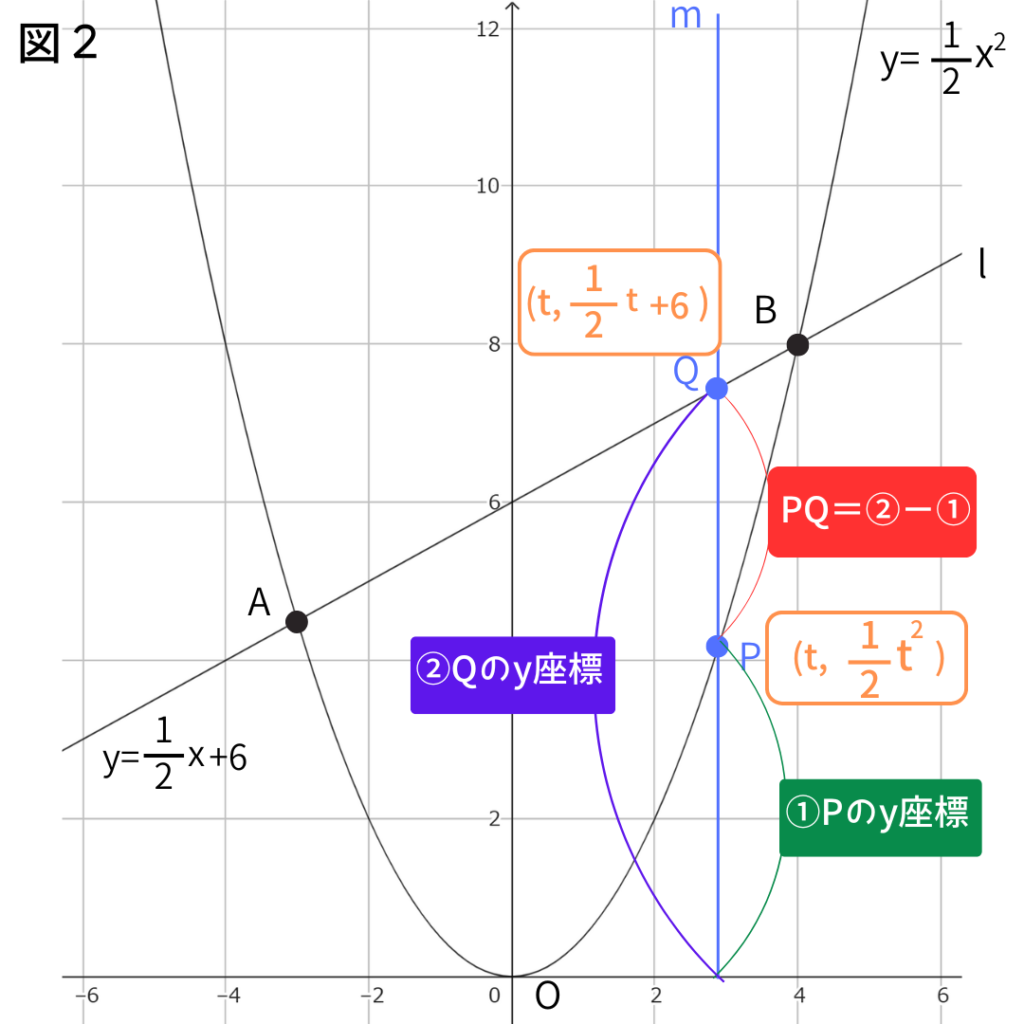
Qのy座標からPのy座標をひいたもの
(Q-P)→PQの長さ
これが3㎝になるので、Q-P=PQ=3
Pの座標は\((t,\dfrac{1}{2}t^2)\)
Qの座標は\((t,\dfrac{1}{2}t+6)\)になる。
Q-P=3なので、
\[\dfrac{1}{2}t+6-\dfrac{1}{2}t^2=3\]
見やすくして
マイナスをかけて
\[\dfrac{1}{2}t^2-\dfrac{1}{2}t-6=-3\]
2倍して \[t^2-t-12=-6\]
整理して \[t^2-t-6=0\]
因数分解して\[(t-3)(t+2)=0\]
\[t=3,-2\]
Pの\(x\)座標を\(t\)としたので、PQが3㎝になるのは\(x\)が-2と3のとき。
Pの座標は\((t,\dfrac{1}{2}t^2)\)と表されるので
\(x=-2\)のとき、\[(-2,2)\]
\(x=3\)のとき、\[(3,-\dfrac{9}{2})\]
よって点Pの座標は\((-2,2)、(3,-\dfrac{9}{2})\)
最後に、点Pがちゃんと点Aと点Bの間に入っていることを確認しよう!
ここはひとりでやっていると
「今自分がなにしてるのかわからない…」
そんなことに陥りがち…
私たちと一緒に解いてみよう!
お問い合わせはこちら







