長野県立高校入試対策問題【数学:問2】
まずはこんな問題から
長野県のある中学校では1年生で1泊2日の高原学校に行く予定です。
【つきのさん】と【そあらくん】はホテルの部屋割りについて話をしています。
【つきのさん】
「ねえ、そあらさん。
高原学校での部屋割りの話を聞いたんだけど、ちょっと面白いの!」
【そあらさん】
「どんな話?」
【つきのさん】
「1年生のクラスで部屋割りをするときにね、1部屋に6人ずつ入れる予定だったんだけど。
そうすると27人も入れないんだって。」
【そあらさん】
「それは結構大変だね。人数が多いのかな?」
【つきのさん】
「うん。それでね、先生たちが考え直して、今度は1部屋に8人ずつ入れるようにしてみたんだって。」
【そあらさん】
「そしたら、ちゃんと入れたの?」
【つきのさん】
「いや、それがまた不思議でね。
今度は3人だけ入った部屋が1部屋と、さらに空き部屋が2つもできちゃったんだって。」
【そあらさん】
「えー、今度は部屋が余っちゃったんだ。
じゃあ、その部屋の数とか人数を考えたら、何か計算できるのかな?」
【つきのさん】
「そう思って、私が部屋の数をx部屋だと考えて方程式を作ってみたの。」
【そあらさん】
「じゃあ、私は1年生の人数を x人だと考えて別の方程式をつくろうかな」
【つきのさん】
「なるほど!
それぞれの考え方で解くっておもしろいかもね。どんな方程式ができるか試してみよう!」
【つきのさん】の考え方
部屋は全部で \(x\) 部屋。だから、1部屋に6人ずつ入ると合計で \(6x\) 人です。
それだと27人も部屋に入れないから
人数は \((6x+27)\)人 だよね。
次に1部屋に8人ずつ入る場合は…
空いてる部屋が ア部屋 あって、3人だけの部屋が1部屋だから
\[6x+27=8(x-ア)+3\]になるね。
【そあらさん】の考え方
1部屋6人ずつにすると27人が入れないから人数 \(x\)人 から27人を引いた \((x-27)\)人 が6人の部屋に入るよね。
これで必要な部屋数がわかるはず。
次に1部屋8人ずつにすると、1部屋は3人だけで、2部屋あまる。
つまり、人数 \(x\)人 から3人引いた \((x-3)\) が8人ずつの部屋にはいる。
そこに残りの部屋も含めると
\[\dfrac{x-27}{6}=\dfrac{x-3}{8}+イ\]
となるよ。
(1)つきのさん、そあらさんが考えた方程式のア、イに当てはまる数を書きなさい。
【ポイント】
文章を表にしっかり整理して、一目でわかるようにすること。
これで文章を何回も読む手間もなくなるし、時間も短縮できるよ。
まずは【つきのさん】
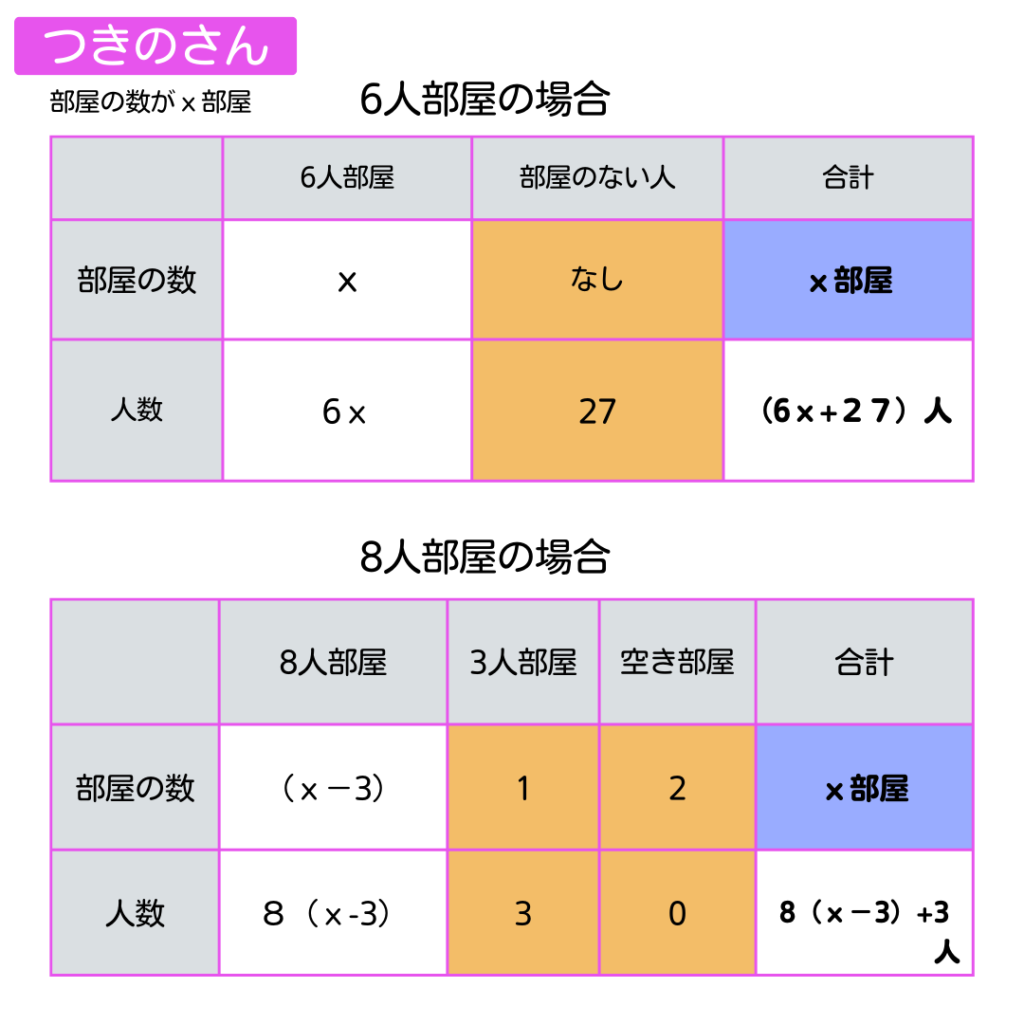
【つきのさん】は
部屋数をx部屋として、1年生の人数をxを使って2通りで表してるよ。
1年生の人数は同じだから=でつないでる。
2通りの表し方を表にするとこんな感じ。
まずは数字で入れていけるところ
(オレンジマス)を記入しよう。
次にx部屋にならないといけないからそこ
(青マス)を記入。
あとは表の上下と前後の関係から穴埋め
(白マス)していこう。
こうすれば、問題を何回も読む必要もなくなるよ。
よって\[\large{アは3}\]
次は【そあらさん】
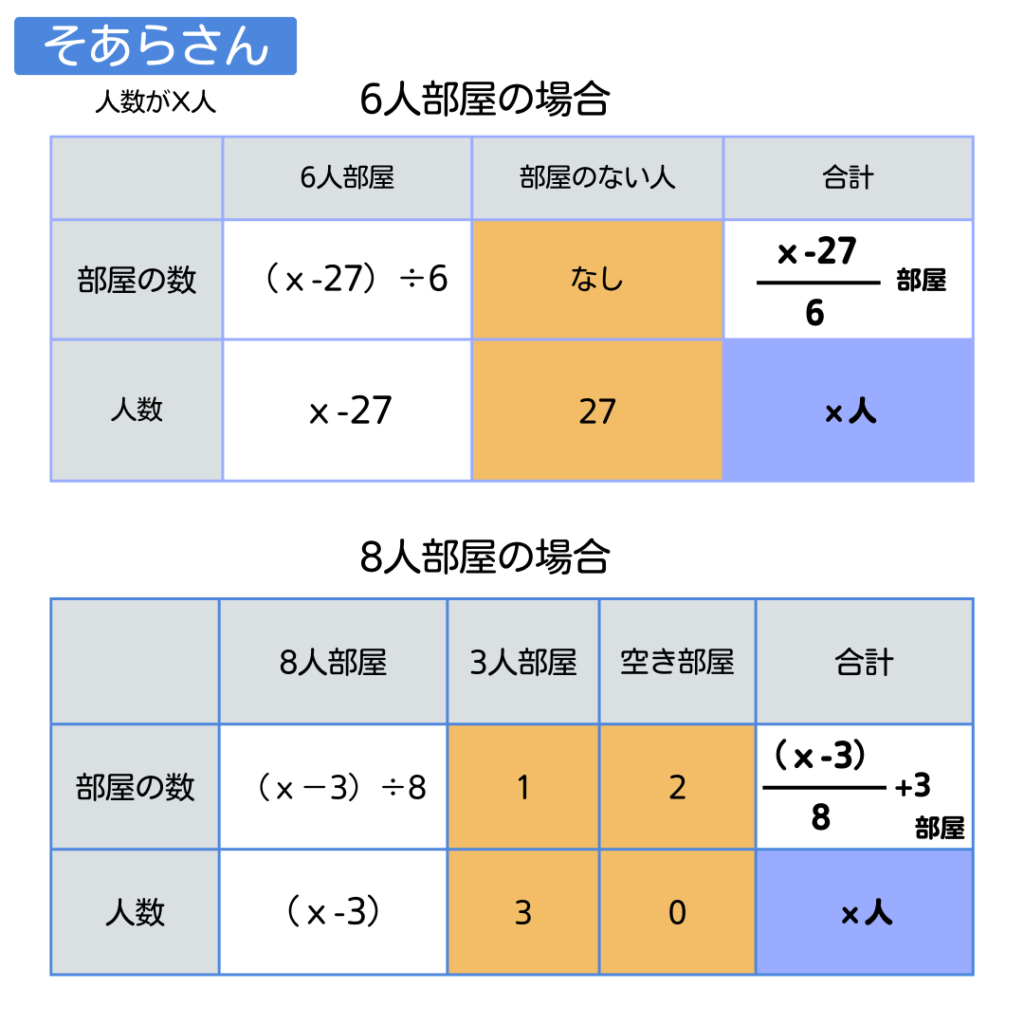
【そあらさん】は
人数をx人として、部屋の数xを使って
2通りの表し方をしてる。
部屋の数は同じだから=でつないでる。
こっちもこんな感じ。
まずは数字で入れていけるところ
(オレンジマス)を記入しよう。
次にx部屋にならないといけないからそこ
(青マス)を記入。
あとは表の上下と前後の関係から穴埋め
(白マス)していこう。
何を文字で置いているのかそこだけは
しっかり確認!
そうしないと全部間違っちゃうからね。
よって\[\large{イは3}\]
(2)部屋の数とこの中学校の1年生の人数を求めなさい。
【ポイント】
式はできてるからあとは計算あるのみ。
分数はどうしてもミスをしやすい。
だから、方程式が2つ以上あったら、できれば分数がない式で計算しよう。
部屋の数は【つきのさん】を計算しよう!\[6x+27=8(x-3)+3\]
まず()をはずす。\[6x+27=8x-24+3\]
次は計算してから移項するよ。
ひとつずつ丁寧に!\[6x+27=8x-21\]
\[6x-8x=-21-27\]
\[-2x=-48\]
\[x=24\]
よって\[\large{部屋の数は24}\] ★次は人数
【つきのさん】の6人部屋の場合を計算!\[6x+27\]
に \(x=24\) を代入しよう。\[6×24+27=171\]
よって\[\large{1年生の人数は171人}\]
人数は【そあらさん】を計算してもできるよ!
2問目はこんな問題
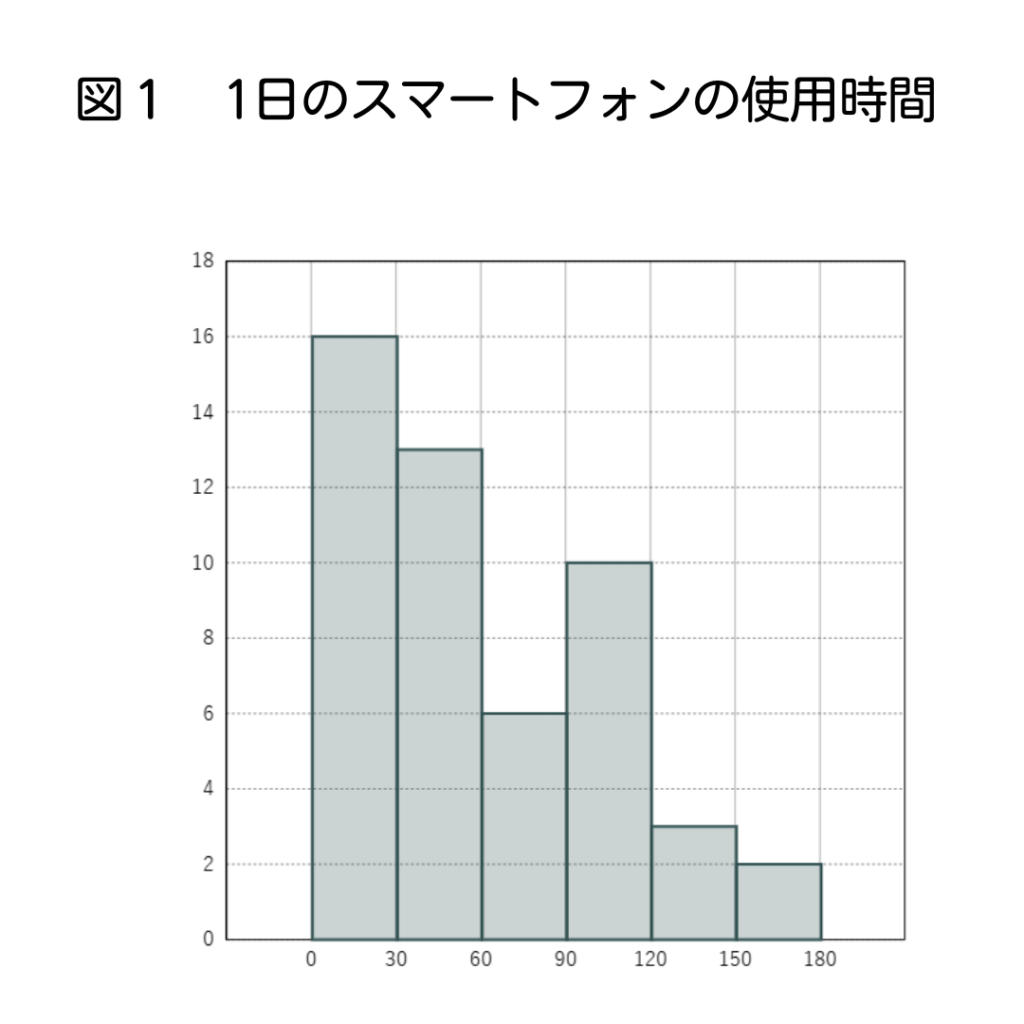
しゅんぺいさんは、A中学校3年生の生徒50人を対象に、1日のスマートフォンの使用時間を調べることにした。
図1はそのデータをヒストグラムに表したものである。
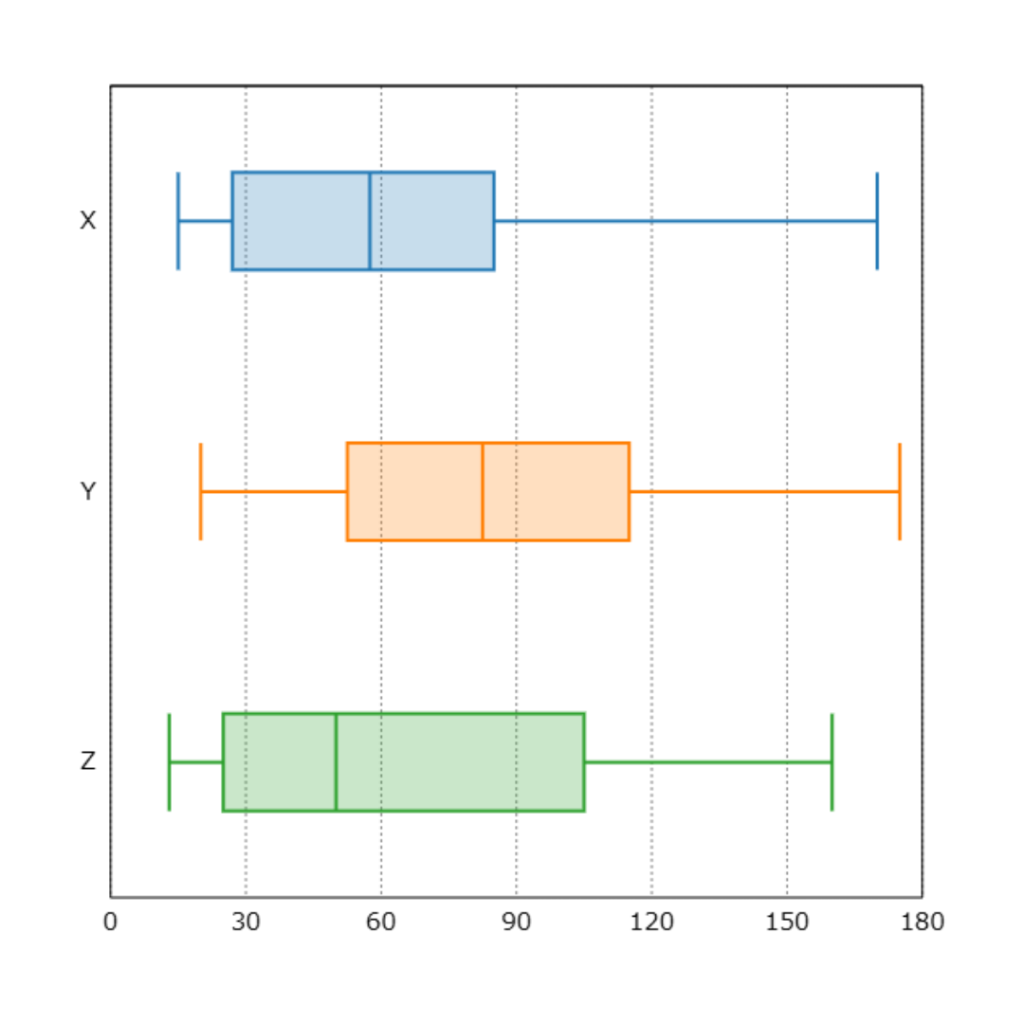
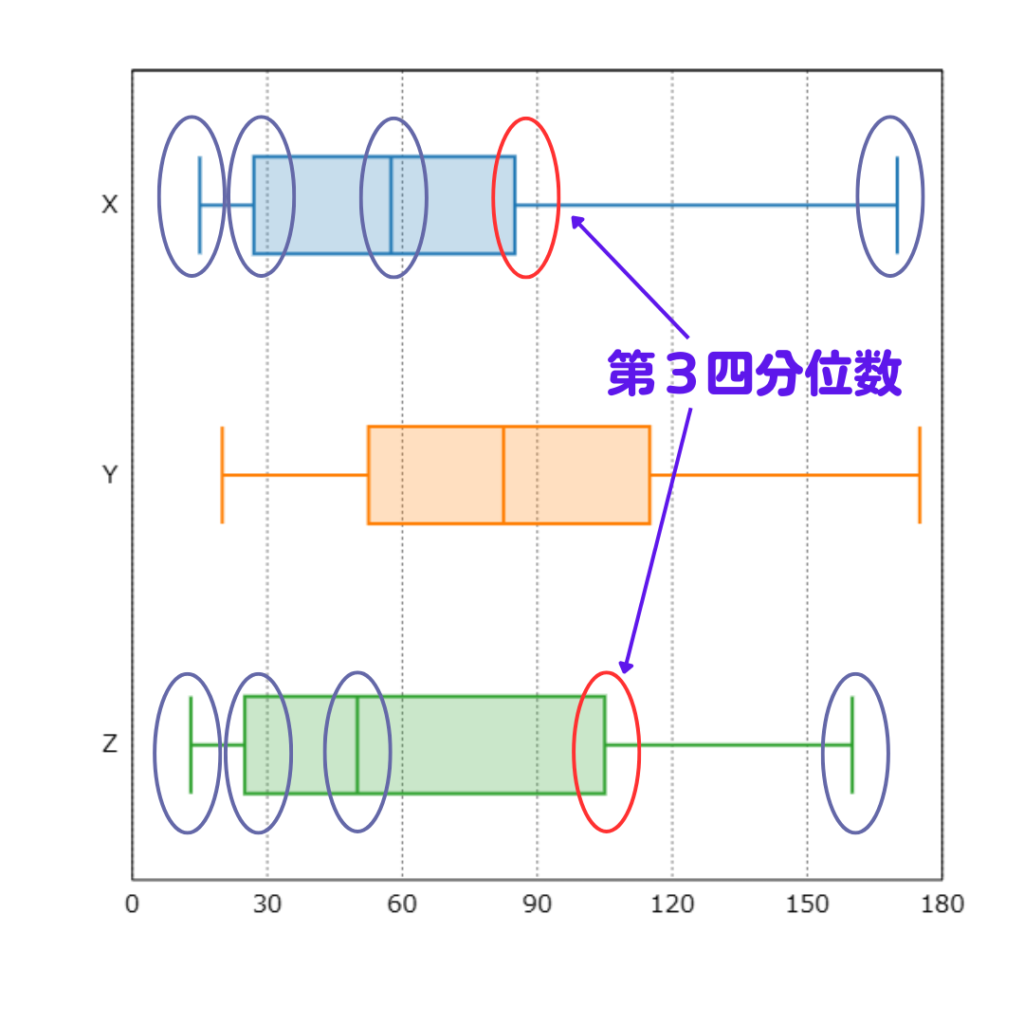
(1)図1のヒストグラムを箱ひげ図に表したものとして正しいものを、下の図X~Zの中から一つ選びなさい。
【ポイント】
ヒストグラムのかたよりと箱ひげ図のかたよりは同じ傾向にあることが多いよ!
問題では、ヒストグラムは左に偏ってるよね。
だから箱ひげ図も左に偏るはず。
これで箱が右に寄ってるYは違うって判断できる。
あとはXとZの違いを考える。
最小値、第1四分位数、中央値、最大値を見るとXとZともに同じ階級に入ってる。
つまり、ここからの判断はできないよ。
第3四分位数のみ違う階級にある。
だから、ヒストグラムから第3四分位数が含まれる階級を求めよう。
すると…
90分以上120分未満の階級に含まれるから
答えはZということだね。
箱ひげ図の四分位数の求め方でもう一度確認してみよう!
(2)図1のヒストグラムについて正しく述べたものを次のア~エからすべて選びなさい。
ア:1日あたりの使用時間が120分以上150分未満の相対度数は0.06である。
イ:A中学校のスマートフォンの使用時間の平均値は61.2分である。
ウ:中央値が含まれる階級は60分以上90分未満である。
エ:半分以上の生徒が60分以上スマートフォンを使用している。
【ポイント】
こういったタイプの問題はひとつひとつ検証していくのが遠いようだけど正解への近道!
\[相対度数=その階級の人数÷全体の人数\]
だから、\[3÷50=0.06\]
よってアは正解。
次はイ:
ここは平均値。これが一番手間がかかるね。
階級の幅があるから、まずは階級値を求めよう。
それぞれの階級で\[(階級値×人数)\]をしよう。
平均値は\[(それぞれの階級値×人数)の和÷全体の人数\]
よって\[\scriptsize{(15×16+45×13+75×6+105×10+135×3+165×2)÷60}\]
\[=61.2\]
だからイも正解。 次はウ:
中央値の問題だね。
50人のちょうど真ん中のひとはどの階級でしょう?って話だね。
ちょうど真ん中は25.5人。
0.5人はいないから、25番目と26番目のヒトをチェック!
そうすると・・・
両方30分以上60分未満の階級に入ってることが分かるよ。
だからウは不正解。 最後にエ:
60分以上スマホを使ってる人の数を数えよう。
ヒストグラムから
60分以上90分未満が6人
90分以上120分未満が10人
120分以上150分未満が3人
150分以上180分未満が2人
この21人が60分以上スマホを使用してる人数。
人数は50人なので、半分以上ではないね。
よって、エも不正解。
これらから正解はアとイになる。
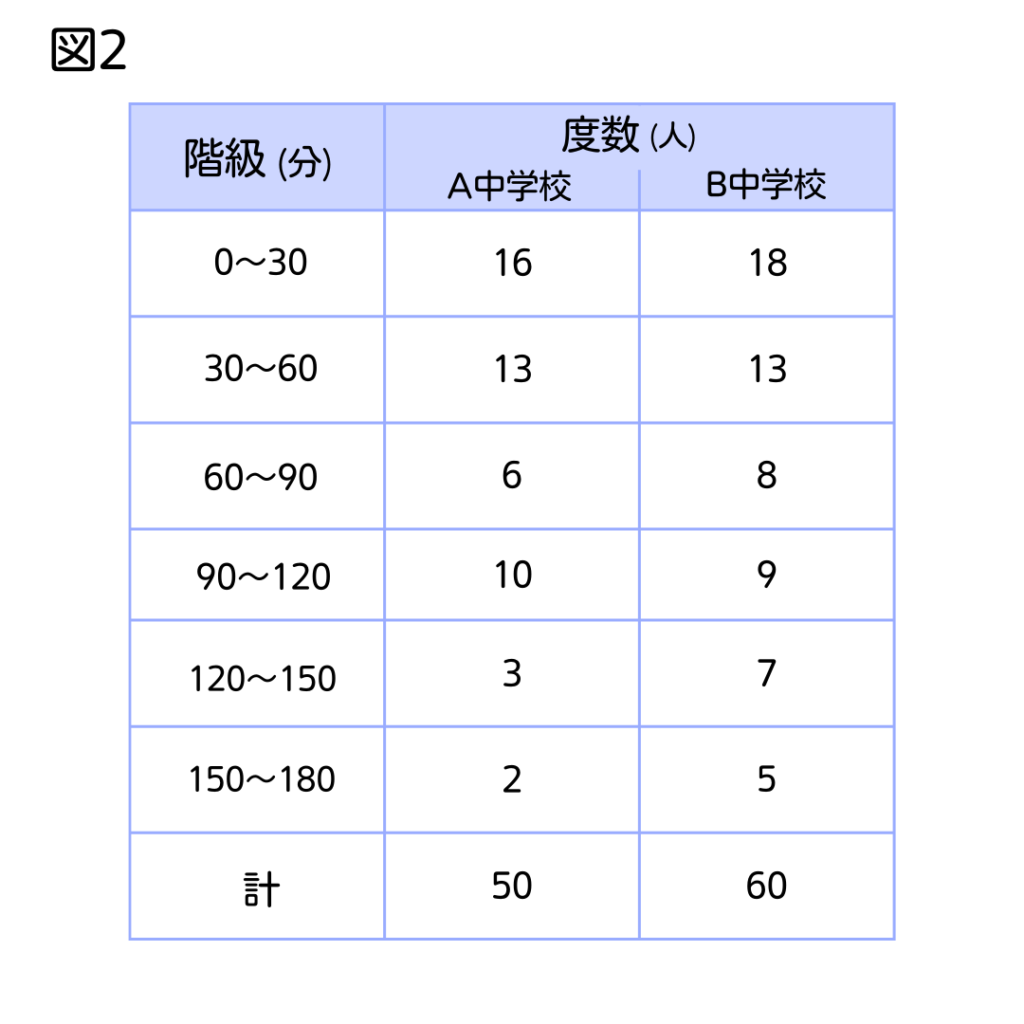
(3)しゅんぺいさんはB中学校3年生60人にも同様の調査を行い、A中学校とB中学校を比較するために図2のように度数分布表にまとめた。
しゅんぺいさんは"度数分布表から1日あたりのスマートフォンの使用時間が90分未満の生徒の割合はB中学校のほうが大きい"と判断した。
これは正しいと言えるかどうか、「累積相対度数」という言葉を用いて説明しなさい。
【ポイント】
“何かを用いて説明しよう。"タイプの問題は用いる言葉を素直に求めてみよう。
だからこの問題は、「累積相対度数」を求めてみよう!
問題には、90分未満の生徒の累積相対度数って書いてある。
だからA中学校とB中学校でそれぞれ求めてみる!
\[その階級までの累計人数が全体のどれだけか\]
これが累積相対度数だね。
A中学校:\[(16+13+6)÷50=0.7\]
B中学校:\[(18+13+8)÷60=0.65\]
だから、A中学校のほうが割合は大きい。
つまり、しゅんぺいさんは正しくないってこと。
解答はしっかり書くこと。こんな感じ。
★スマートフォンの使用時間が90分未満の累積相対度数が、A中学校は0.7、B中学校は0.65なので
A中学校のほうが大きい。
だから、しゅんぺいさんは正しくない。
人数の大きさと割合の大きさは異なることが多いから、覚えておくこと。
これで最後、3問目の問題
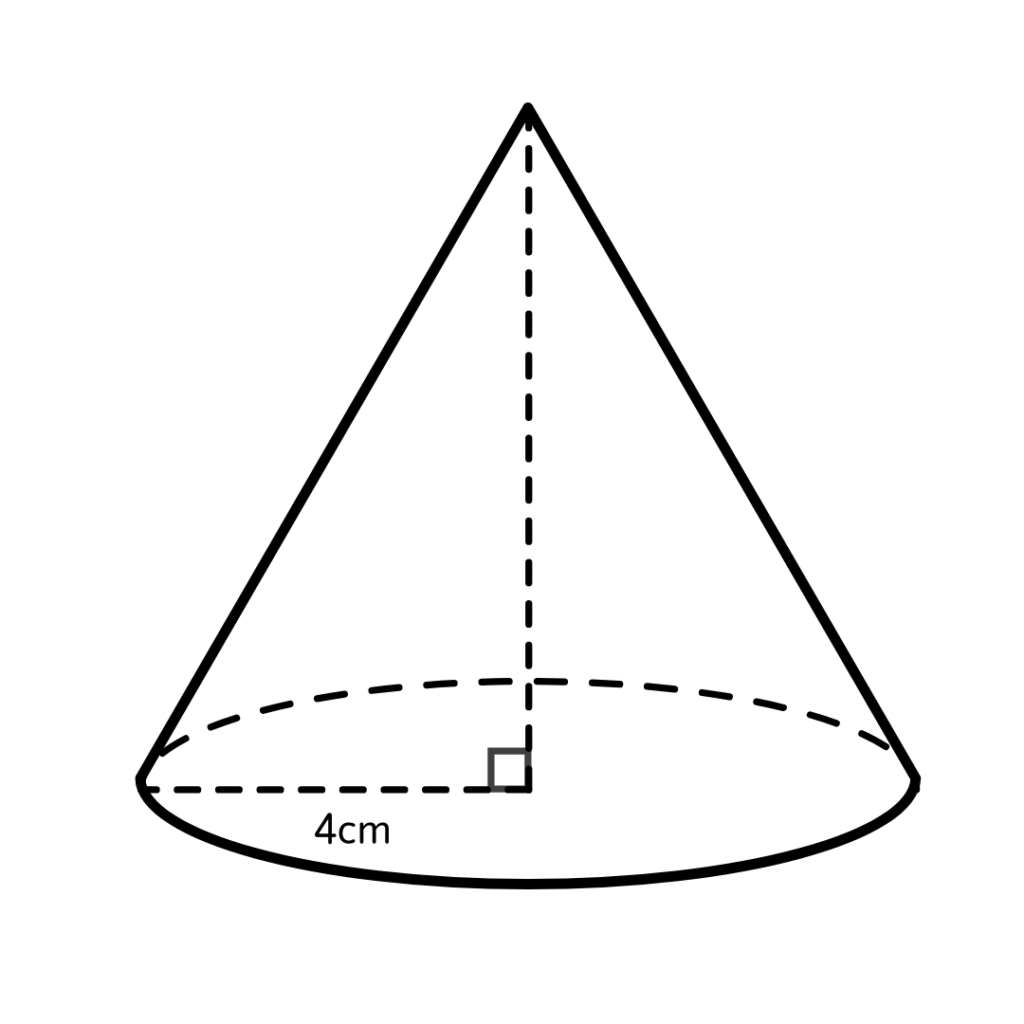
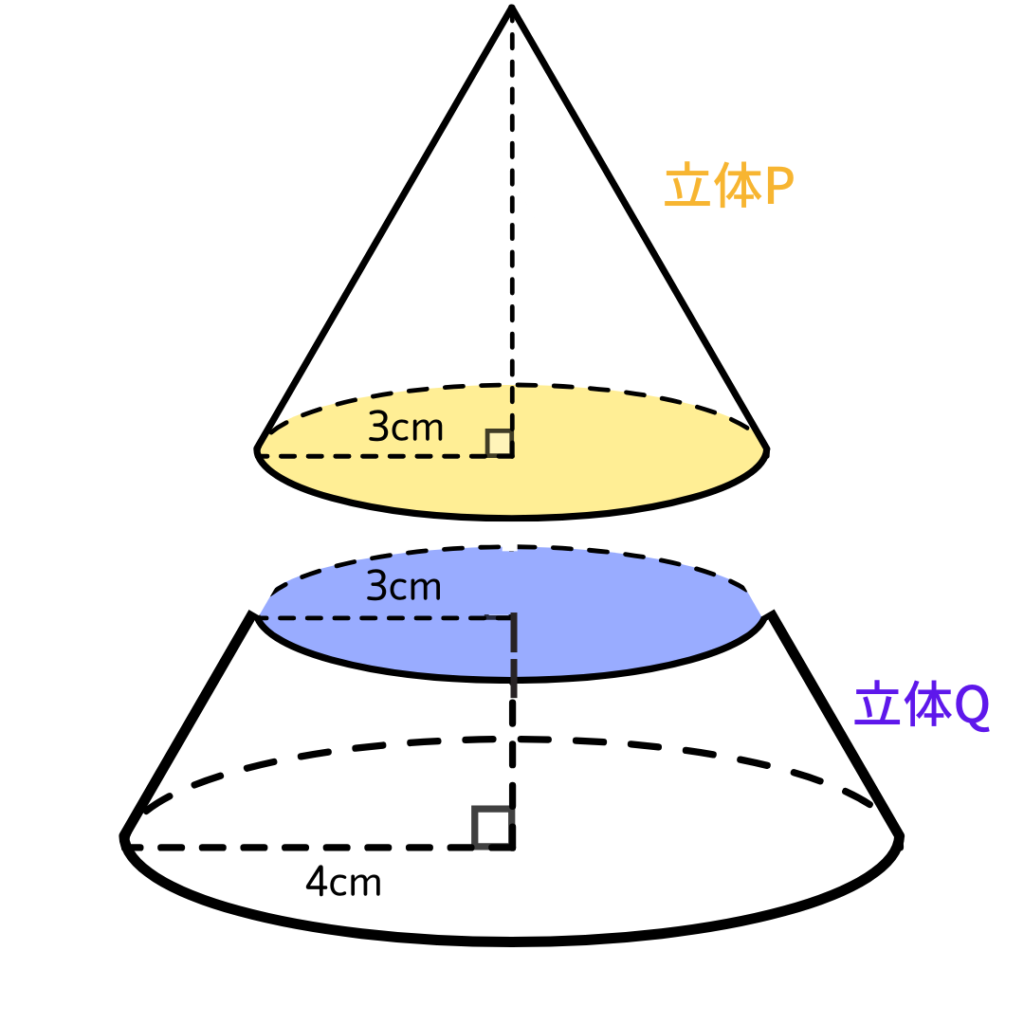
図のような底面の半径が4cmの円すいがある。
この円すいを底面に対して水平な面で切断したときのそれぞれの体積についてみんなで考えることにしました。
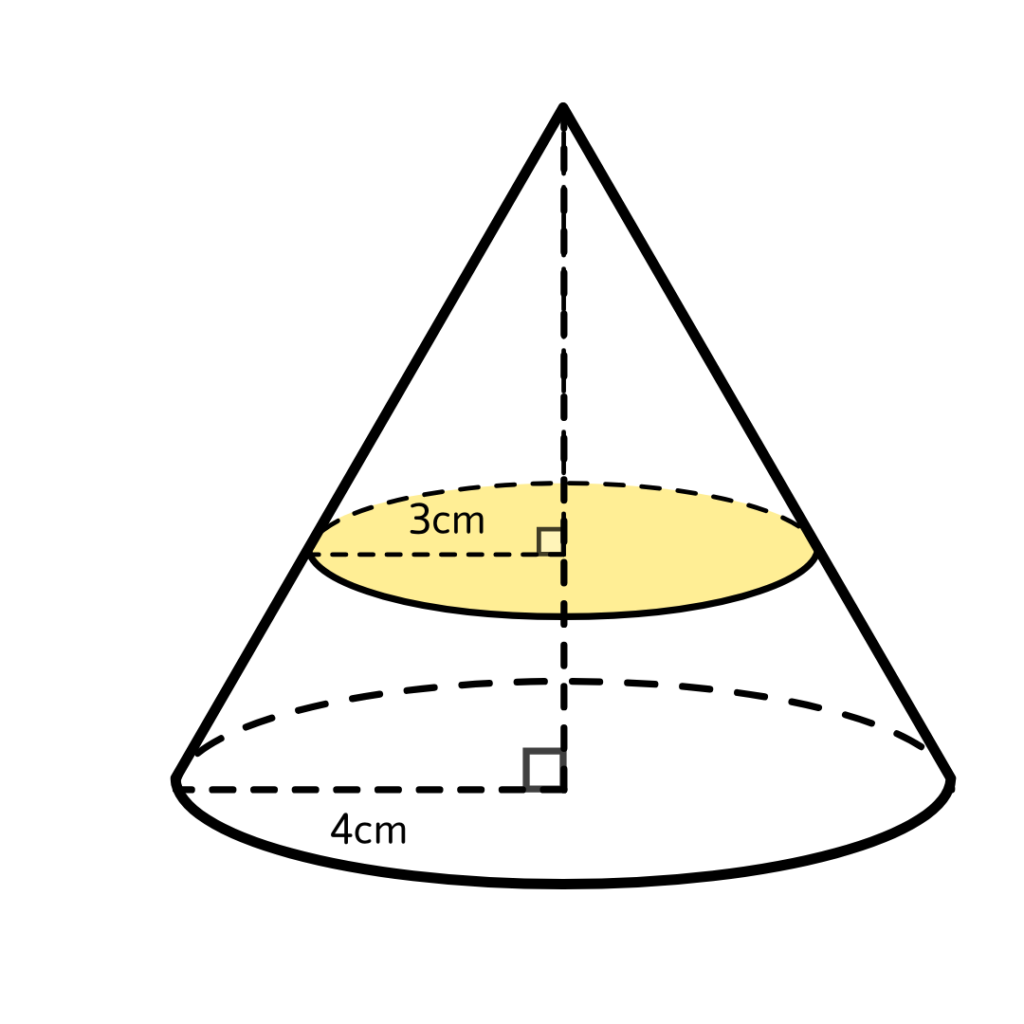
底面に対して水平に切ったとき、下図のように切断面の半径はちょうど3cmでした。
切断した上側の立体をP、下側の立体をQとしました。
このとき、立体Pと立体Qの体積比を求めなさい。
【ポイント】
体積比っていうコトバが出たら相似比を使って考えることが多いよ。
体積の公式を使ってそれぞれの体積を求めることができなかったら、ほぼこのパターンだね。
\[面積比\quad a^2:b^2\quad \]
\[体積比\quad a^3:b^3\quad \]
これは覚えておこう!
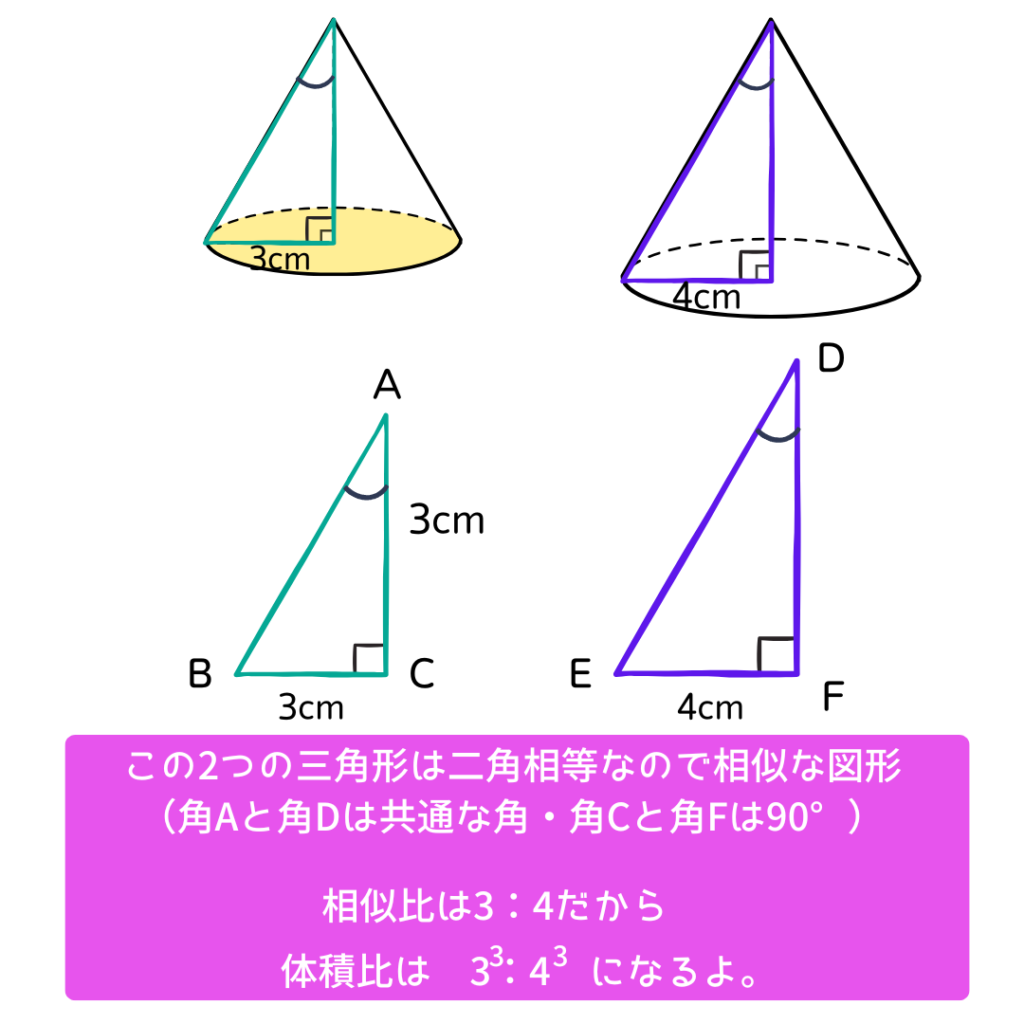
もとの円すいを縮小していくと立体Pになります。
ってことはもとの円すいと立体Pは相似だね。
では、ここで相似比を考えよう。
下にまとめてあるよ。
でも、立体Pと立体Qの体積比がほしい・・・。
じゃあ、こんな考え方をしてみよう。
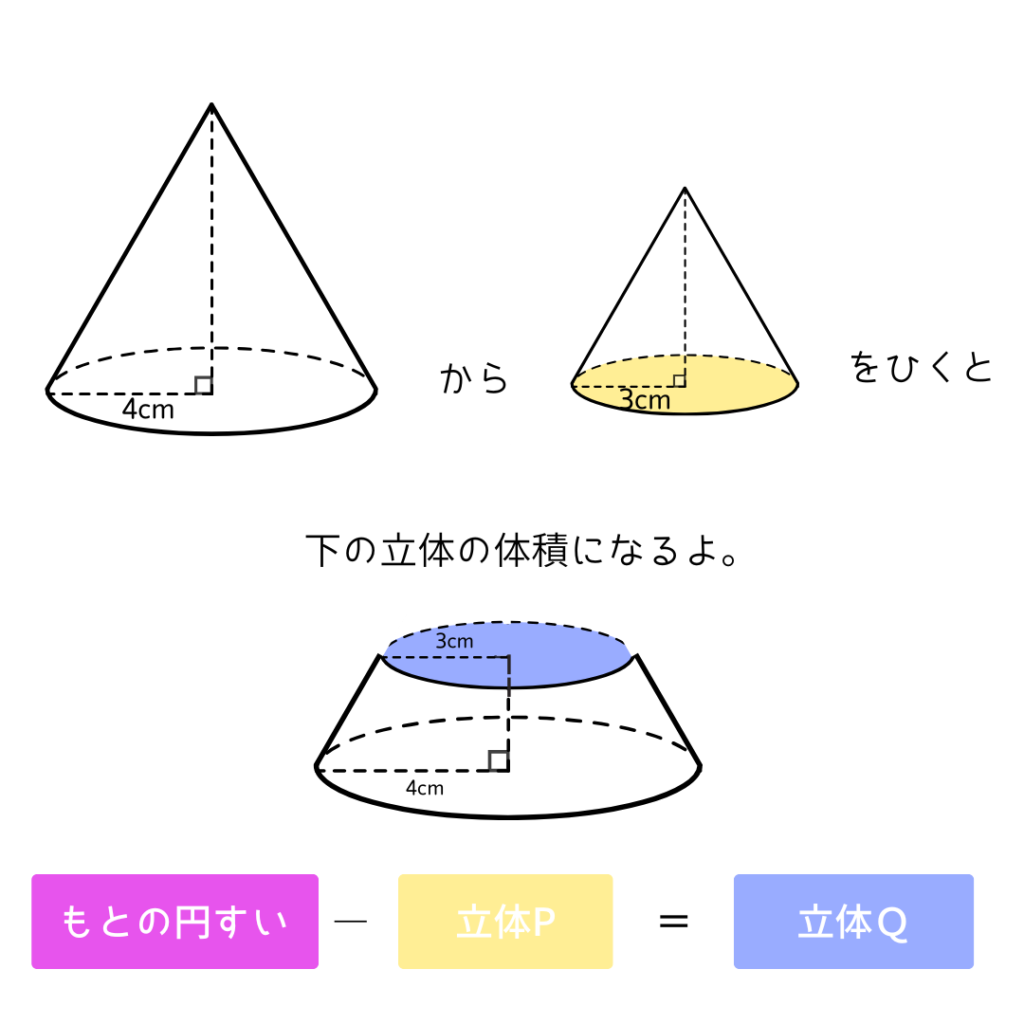
でも、分かりやすく\(\quad 64㎤\quad \)だと仮定しよう。
すると立体Pは\(\quad 27㎤\quad \)になるね。
すると立体Qは\(\quad 64-27=37㎤\quad \)だとわかる。
これでもう答えだね。
立体Pと立体Qの体積比は27:37だね。
ここまで、問2のよく出る問題の考え方・解き方をみてみました。
でも、問2ってもっと多くのパターンの問題がでるよ!
ITTO長野で一緒に解いてみよう!
お問い合わせはこちらから







