中学校1年生数学-図形の移動
単元：図形の移動
今日は図形の移動について学習していくよ。図形を移動させる方法は全部で3つあります。
ひとつずつ確認していきましょう。
ひとつずつ確認していきましょう。
1つ目は、「平行移動」。
平行移動とは、「図形を一定の方向に一定の長さだけずらして移動させること」を言います。
例えば下の図の△DEFは△ABCを平行移動させてできた図形です。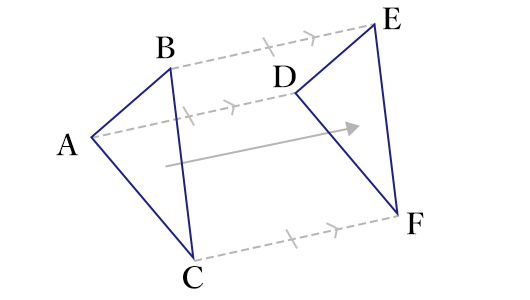
なるほど！平行移動の場合、図形の向きは変わらないんですね。
そうです。
さらに△ABCの各頂点に注目してみてください。
それぞれ同じ方向に同じ長さだけ移動しているということがわかります。
さらに△ABCの各頂点に注目してみてください。
それぞれ同じ方向に同じ長さだけ移動しているということがわかります。
記号で表すと「AD//BE//CF、AD＝BE＝CF」ということですね。
その通り！
それでは2つ目にいきましょう。
次は「回転移動」です。
回転移動とは「図形を1つの点Oを中心として、一定の角度だけまわして移動させること」と言います。
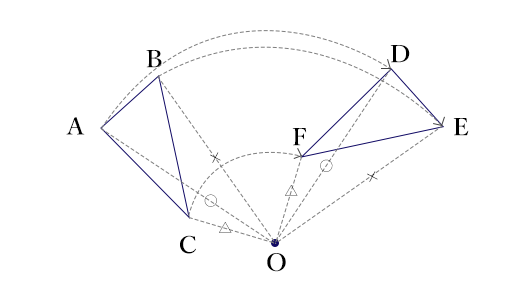
例えば下の図の△DEFは、△ABCを点Oを中心として90度回転させた図形です。
また、この点Oのことを「対称の中心」と言います。
それでは2つ目にいきましょう。
次は「回転移動」です。
回転移動とは「図形を1つの点Oを中心として、一定の角度だけまわして移動させること」と言います。
例えば下の図の△DEFは、△ABCを点Oを中心として90度回転させた図形です。
また、この点Oのことを「対称の中心」と言います。
今度は図形の向きが変わってますね。これも記号で表すことができますか？
いい質問です！重なっているので分りづらいですが、
「OA＝OD、OB＝OE、OC=OF、∠AOD＝∠BOE＝∠COF＝90°」
と表すことができます。
「OA＝OD、OB＝OE、OC=OF、∠AOD＝∠BOE＝∠COF＝90°」
と表すことができます。
なるほど。各頂点の移動を別々に書いてみると下の図のようになりますね。
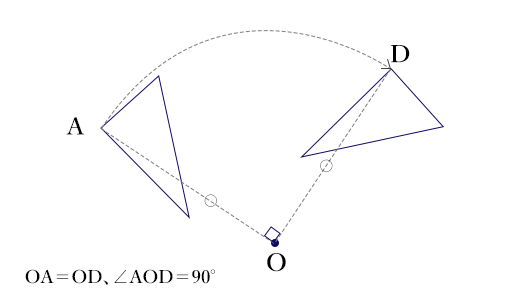
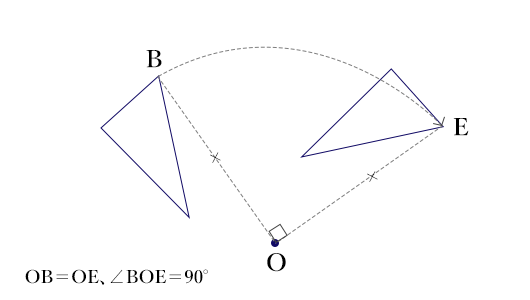
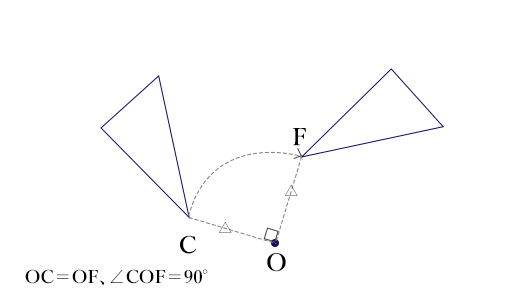
分りやすくて良いですね。
では、今度はこの△ABCを点Oを中心として180°回転させてみましょう。
では、今度はこの△ABCを点Oを中心として180°回転させてみましょう。
えーっと、180°回転させた場合こうなります。
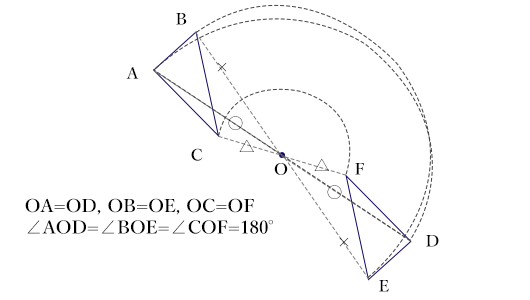
素晴らしい！！よく書けています。
最後は「対称移動」です。
対称移動とは「図形を1つの直線ℓを折り目として、その図形を移動させること」を言います。
下の図の△DEFは、直線ℓを軸として△ABCを対称移動させた図形です。
またこの直線ℓを「対称の軸」と言います。
この図から分かることは、何かあるかな？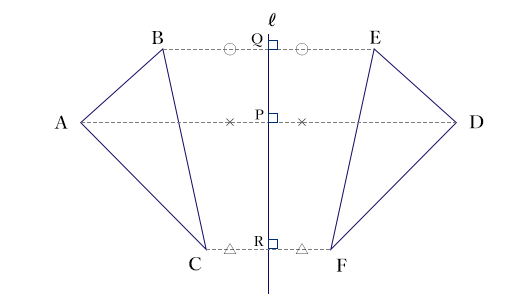
直線ℓが鏡になって、2つの図形が向かい合ってるように見えますね。
図を見ると、線分AD、BE、CFはどれも直線ℓと垂直に交わってます。
また点P、Q、RはAD、BE、CFそれぞれの中点になっています。
図を見ると、線分AD、BE、CFはどれも直線ℓと垂直に交わってます。
また点P、Q、RはAD、BE、CFそれぞれの中点になっています。
その通り！
そのことを記号で表すと「AD⊥ℓ、BE⊥ℓ、CF⊥ℓ、AP＝DP、BQ＝EQ、CF＝FR」
になります。覚えておきましょう！
そのことを記号で表すと「AD⊥ℓ、BE⊥ℓ、CF⊥ℓ、AP＝DP、BQ＝EQ、CF＝FR」
になります。覚えておきましょう！
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。