中学校2年生数学ー連立方程式の利用(池の問題)
単元:連立方程式(池の問題)

さて、今日は次の 文章題に取り組んでみよう。


うーん、 なんだか難しそうだなぁ‥‥。

大丈夫!一緒に解いていきましょう。
まず、兄の速さを分速xm、弟の速さを分速ymとします。
次に 下の図を見て下さい。
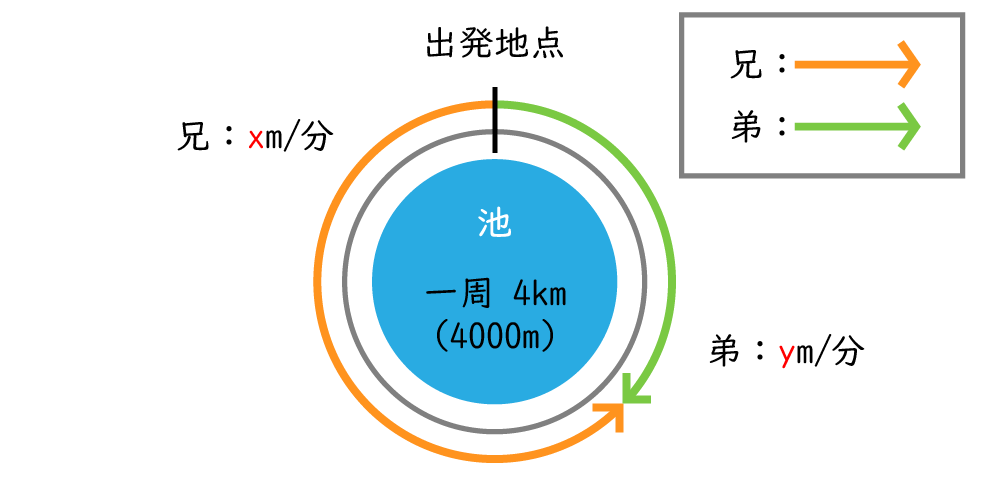
兄と弟が逆方向に出発した場合、
兄の進む道のりと弟の進む道のりを合わせると池1周分の道のりになることが分かります。
2人が出発してから出会うまでの時間は 10分であることから、兄の進む道のりは10x(m)、
弟の進む道のりは10y(m)と表せるので、10x+10y 4000…①
という式が作れます。

なるほど!2人が 逆方向に出発した場合は、
兄が10分間に進む道のり+弟が10分間に進む道のり=池1周分
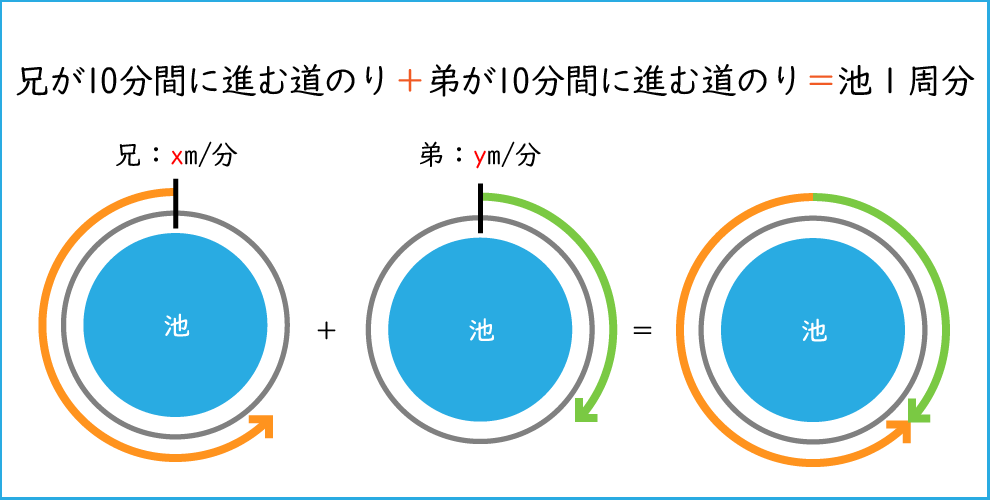
となるのですね!

そうです!
では次に、同じ方向に出発した場合を考えてみましょう。
2人の進む道のりは下の図のようになります。
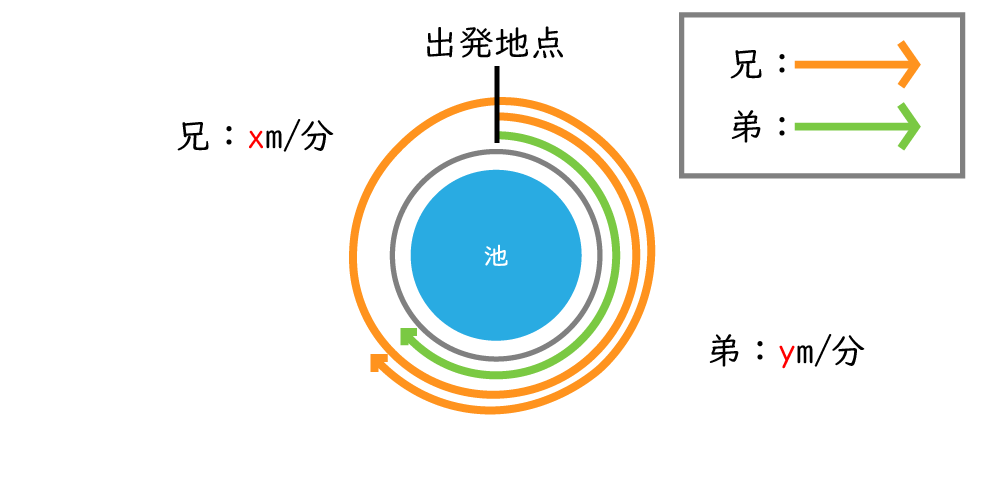
兄は弟より池1周分多く走っているので、
兄が進んだ道のりから弟が進んだ道のりを引くと、池1周分の道のりとなります 。
2人が出発してから兄が1周差をつけて弟に追いつくまでの時間は50分であることから、
兄の道のりは50xm、弟の道のりは50ymと表せるので、50xー50y=4000 …②
という式をつくることができます。

今度は兄が50分間に進む道のりー弟が50分間に進む道のり=池1周分
となるのですね!
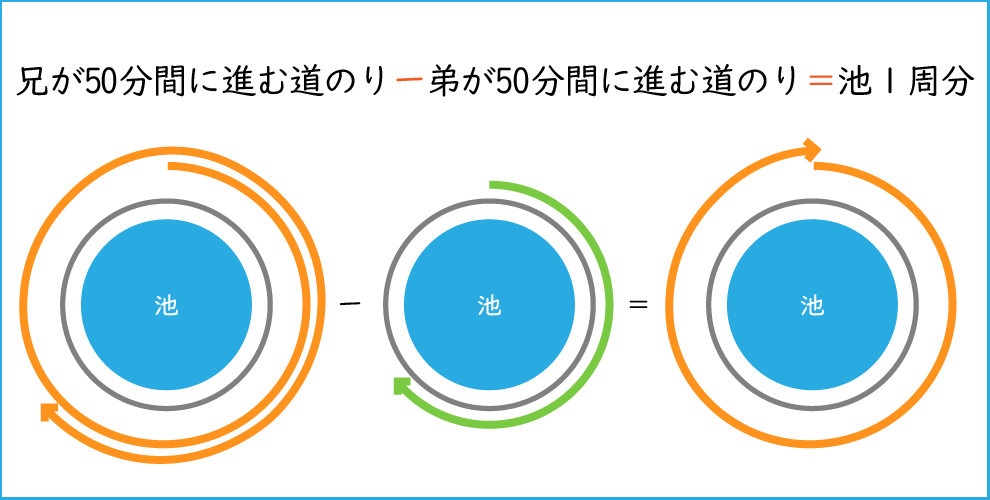

その通りです。
そして①、②を連立方程式として解くと、
x=240, y=160 となるので
答えは
兄…分速 240m 、弟…分速 160m となります。

なるほど!よく分かりました。
長野県長野市の中学生数学特訓プラン
各自の実力と志望高、目的に合わせプランはカスタマイズしてご提案しております。詳しくは各教室まで。
基礎力養成特訓プラン
| 推奨学年 | 中学1年~中学3年生 |
| 内容 | 計算の基礎養成演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生:9,130円(税込) |
| 中学2年生:9,570円(税込) | |
| 中学3年生:9,790円(税込) |
発展力養成特訓
| 推奨学年 | 中学1年~中学3年生 |
| 内容 | 文字式・方程式・関数・証明等の文章題読解演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生:9,130円(税込) |
| 中学2年生:9,570円(税込) | |
| 中学3年生:9,790円(税込) |









