【中1】方程式の利用(規則性)
単元:方程式の利用(規則性問題)の解き方

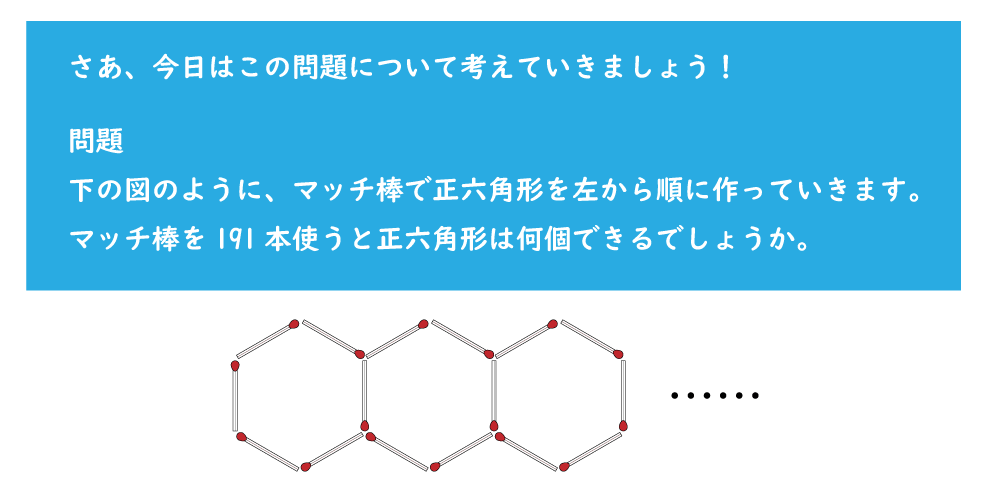

うーん…。191本を全部並べて数えるのは時間がかかりそうですね。
簡単に求める方法ないのかなぁ?
簡単に求める方法ないのかなぁ?

ありますよ!
一緒に考えて行きましょう。
一緒に考えて行きましょう。
下の図を見て下さい。
はじめにマッチ棒が1本あれば、5本増やすごとに正六角形が一個ずつ出来ていきます。
正六角形を作るのに必要なマッチ棒の数は、1+5×n = 5n+1(本)と表すことができます。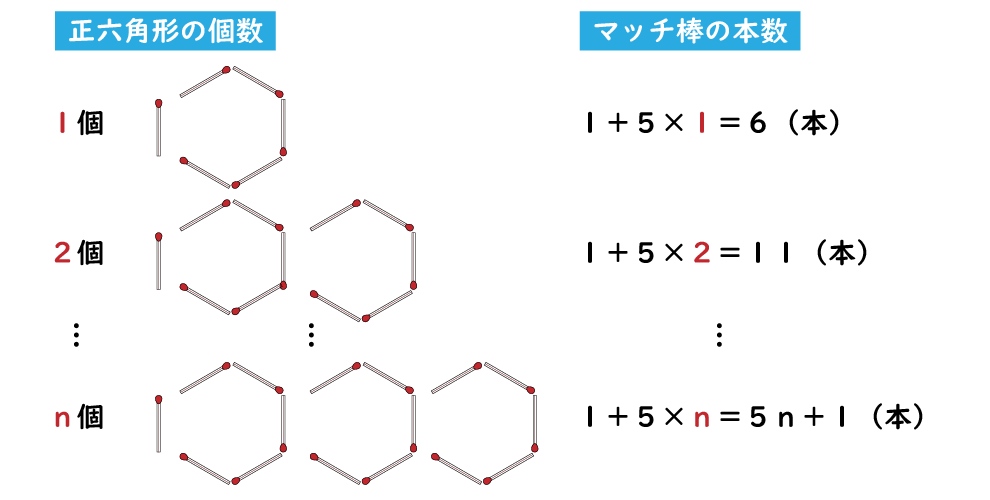

なるほど!
ということは、 5n+1=191 のnを求めればよいから、
5n+1=191
5n = 190
n=38
よって正六角形は38個できます!
ということは、 5n+1=191 のnを求めればよいから、
5n+1=191
5n = 190
n=38
よって正六角形は38個できます!

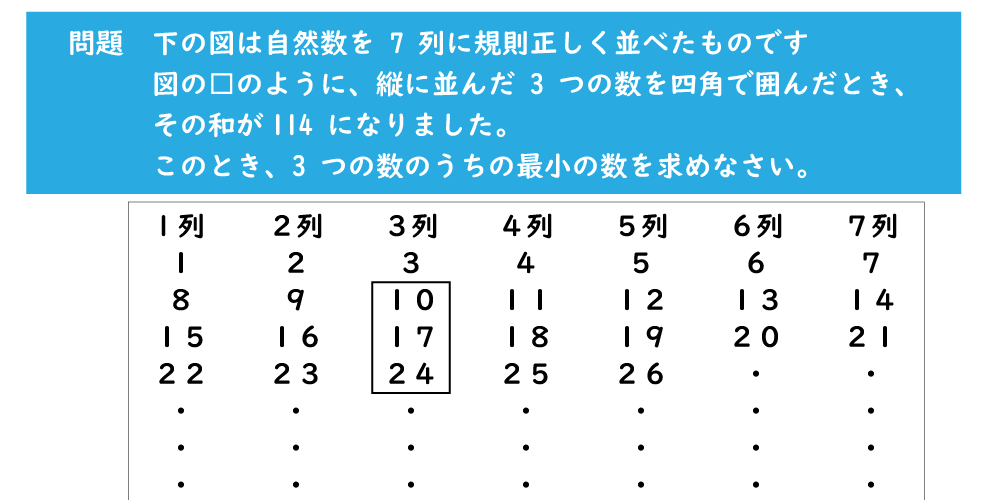
うーん。どこを □ で囲っても、上から 7 ずつ数が大きくなっていますね。この規則性は何か使えそうな気がします。

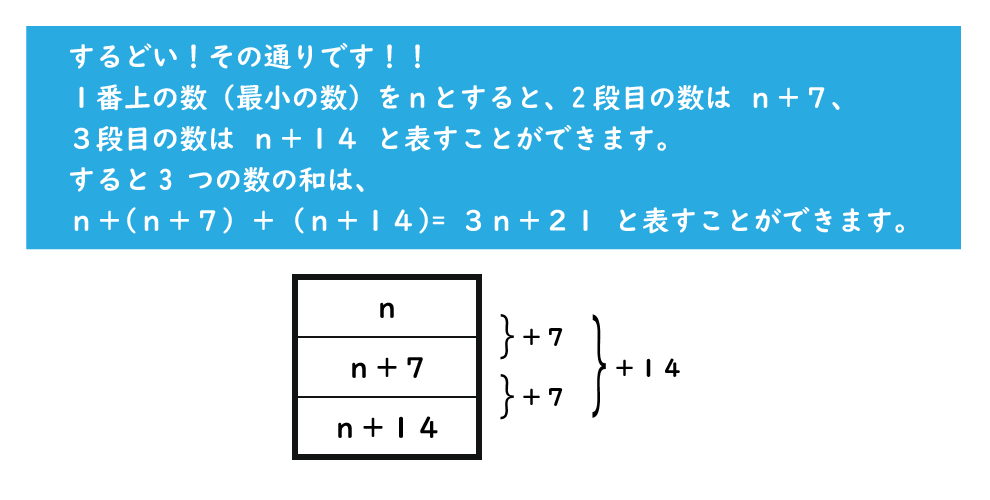

ということは、3n+21=114 になる時のnの値を求めればよいから、
3n+21=114
3n=93
n=31 よって最小の数は、31となります。
3n+21=114
3n=93
n=31 よって最小の数は、31となります。

OK!!よくできました。
他にも規則性の問題はたくさんあるので、色々な問題にチャレンジしてみましょう!
他にも規則性の問題はたくさんあるので、色々な問題にチャレンジしてみましょう!
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで