中学校2年生数学-1次関数の利用（水槽）
単元：1次関数の利用（水槽）の解き方
問題
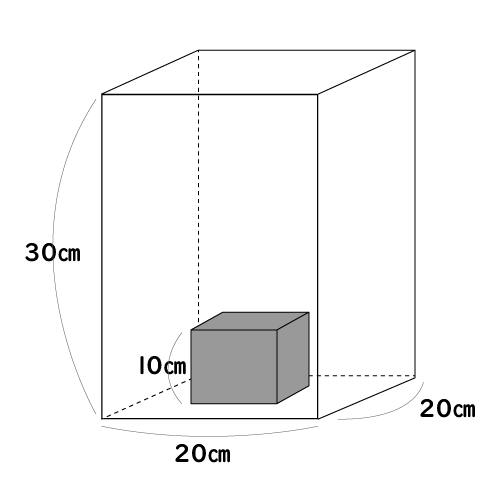
下の図のように、縦20㎝、横20㎝、高さ30㎝の容器があります。
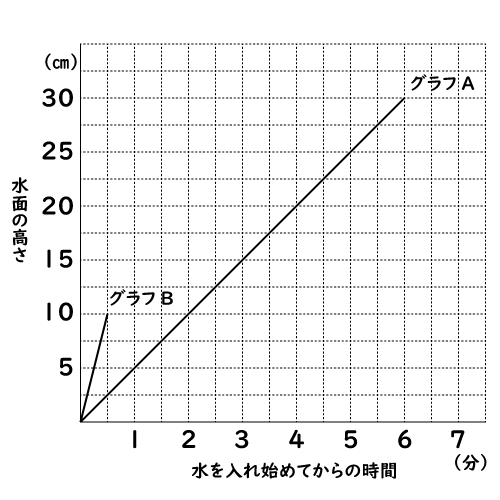
毎分2,000㎥の割合で空の容器に水を入れたときのグラフをAとします。
また、高さ10㎝の鉄の直方体を容器の底に沈め、同様に毎分2,000㎥の割合で水を入れたときのグラフをBとします。
（1） 鉄の直方体の底面積を求めなさい。
（2） 鉄の直方体を入れた容器の場合、高さ10㎝からの続きのグラフを書きなさい。
（3） 鉄の直方体を入れたとき、水が一杯になるまでの時間は何分何秒か求めなさい。
上の問題を解いてみましょう。
まずは、容器と鉄の直方体の隙間に高さ10㎝までに溜まる水の量を考えてみてください。
グラフＢから、直方体の高さ10㎝水が溜まるのに0.5分かかるのが分かります。
毎分2,000cm3の割合で水が入るから、容器と鉄の直方体の隙間に高さ10㎝までに溜まる水の量は、2000×0.5で、1000cm3です。
毎分2,000cm3の割合で水が入るから、容器と鉄の直方体の隙間に高さ10㎝までに溜まる水の量は、2000×0.5で、1000cm3です。
OKです！
次に容器と鉄の直方体の隙間の容積から考えてみましょう。
ヒントは、水の体積（1000cm3）と、容器と鉄の直方体の隙間の容積は等しくなりますよね。
次に容器と鉄の直方体の隙間の容積から考えてみましょう。
ヒントは、水の体積（1000cm3）と、容器と鉄の直方体の隙間の容積は等しくなりますよね。
容器と鉄の直方体の隙間の容積 ＝（高さ10cmまでの容器の容積）－（鉄の直方体の容積）と表せるので
鉄の直方体の底面積をＳcm2とすると、
1000cm3＝（20cm×20cm×10cm）－（Ｓcm2×10cm）
1000 ＝ 4000 － 10Ｓ
10Ｓ ＝ 4000 － 1000
10Ｓ ＝ 3000
Ｓ ＝ 300
問題（1）の答えは、300cm2です。
鉄の直方体の底面積をＳcm2とすると、
1000cm3＝（20cm×20cm×10cm）－（Ｓcm2×10cm）
1000 ＝ 4000 － 10Ｓ
10Ｓ ＝ 4000 － 1000
10Ｓ ＝ 3000
Ｓ ＝ 300
問題（1）の答えは、300cm2です。
正解です！
では、問題（2）の鉄の直方体を入れた容器の場合、高さ10㎝からの続きのグラフを考えてみましょう。
では、問題（2）の鉄の直方体を入れた容器の場合、高さ10㎝からの続きのグラフを考えてみましょう。
はい！
高さ10cm以降は、鉄の直方体に関係なく、1分あたり2000cm3ずつ水が溜まるので、グラフＡと同じく1分あたり5cmの割合で高さが上昇していくので、同じ傾きと考えればいいのかな？
高さ10cm以降は、鉄の直方体に関係なく、1分あたり2000cm3ずつ水が溜まるので、グラフＡと同じく1分あたり5cmの割合で高さが上昇していくので、同じ傾きと考えればいいのかな？
良い調子です！
そうすると、下のグラフが（2）の答えです。
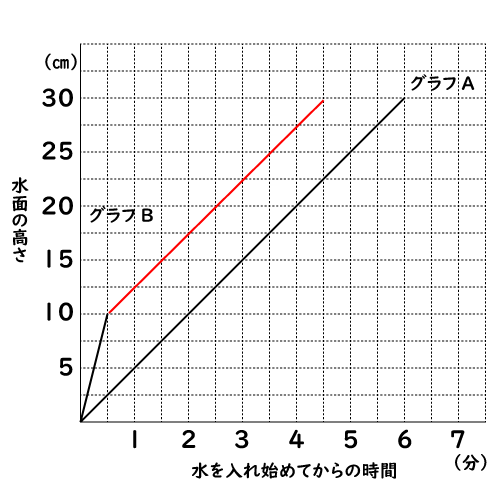あ、問題（3）もグラフから解けちゃった！
問題（3）の答えは、4分30秒です。
あ、問題（3）もグラフから解けちゃった！
問題（3）の答えは、4分30秒です。
素晴らしい！！正解です！
でも、グラフを書くときは、（x.y）座標に必ず黒点を入れてから、その軌跡を定規で正確に書きましょう。
0.5分以降の傾きがグラフＡと平行になっているかも確認すると良いですね。
でも、グラフを書くときは、（x.y）座標に必ず黒点を入れてから、その軌跡を定規で正確に書きましょう。
0.5分以降の傾きがグラフＡと平行になっているかも確認すると良いですね。
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。