中学校3年生数学ー因数分解(おきかえ)

今日は因数分解の応用問題を解いていくよ。
最初の問題はこちらです。
最初の問題はこちらです。
問題
次の式を因数分解しなさい。
(1) a(a+2)-5(a+2)
(2) a(b-c)-b+c
(3) xy+2x-3y-6

(1)は、a+2が2つあるので、これを利用しそうですね。

その通りです。(1)ではa+2を1つの文字におきかえて考えてみます。
すると下のように因数分解をすることが出来ます。

すると下のように因数分解をすることが出来ます。


同じ式の部分を1つの文字におきかえて共通因数でくくるのですね。
では(2)はどのようにして因数分解するのでしょうか。
では(2)はどのようにして因数分解するのでしょうか。

(2)はまず-b+cの部分を-(b-c)の形にします。その後は(1)と同じ流れです。



なるほど。そうすると(3)も(1)と同じような形の式にして解けそうです。
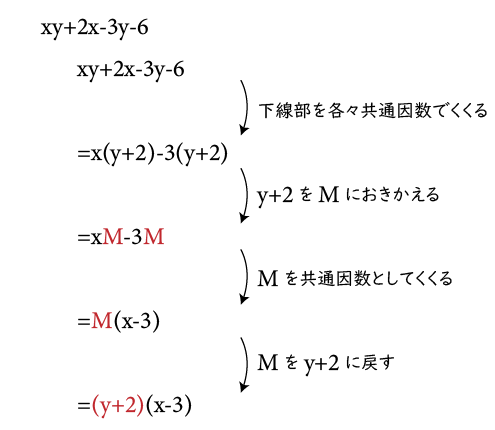
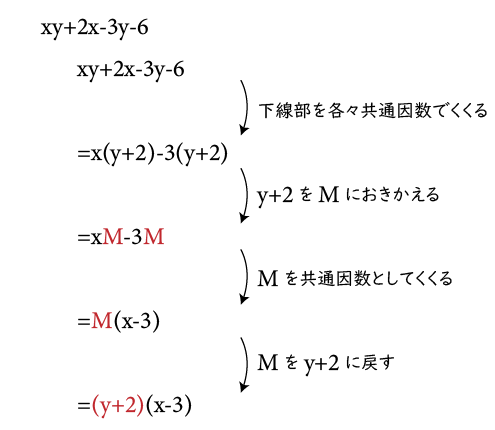

すばらしい!正解です。
このように式の一部分を共通因数でくくってから、文字におきかえて因数分解をするパターンもありますので、よく覚えておきましょう。
では次の問題です。
このように式の一部分を共通因数でくくってから、文字におきかえて因数分解をするパターンもありますので、よく覚えておきましょう。
では次の問題です。
問題
次の式を因数分解しなさい。
(4) (x+y)2+5(x+y)+6
(5) (a2+4)2-25

(4)は、x+yを文字におきかえて考えると良さそうです。

その通りです。x+y を文字におきかえて因数分解をすると、下のようになります。



なるほど。今度は文字におきかえた後、因数分解の公式を使って解くパターンですね。
(5)も同じような考え方でしょうか。
(5)も同じような考え方でしょうか。

そうですね。(5)では、a2+4を文字におきかえて考えます。



おきかえた文字を元に戻した後、カッコ内の同類項をまとめたり、そのあとさらに因数分解したりしなくてはいけない所が(4)と違いますね。

そうですね。このように、おきかえを利用して考える因数分解の問題にも色々なパターンがあります。
どんな問題が出ても正確に解けるように、たくさん練習しておきましょう。
どんな問題が出ても正確に解けるように、たくさん練習しておきましょう。
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで









