長野県立高校入試対策問題【数学:問1】
今回は数学の問1のよく出る問題と解き方をみていこう!
(1)3-2×(-6)
四則(たし算・引き算・かけ算・わり算)計算の順番の確認をしておこう。
①かっこのなか②かけ算・わり算(乗除)③たし算・引き算(加減)です。
わり算はかけ算にしてから計算するといいよ。
\[3-2×(-6)\]
\[=3-(-12)\]
うしろのかっこを外すよ。
かっこの前がマイナスだから符号は逆になるね。
\[=3+12\]
\[=15\]
はい終了!
計算の順番とかっこのはずし方を気をつけよう!
分数に文字がついてるタイプは必ず文字を分子(うえ)に置いた形にしてから考えよう!
\[\dfrac{3x^2y}{5}÷\dfrac{3xy^2}{4}\]こうするとわり算をかけ算にするときに分かりやすいよ!
では分母と分子を逆にして
\[=\dfrac{3x^2y}{5}×\dfrac{4}{3xy^2}\]
\[=\dfrac{3x^2y×4}{5×3xy^2}\]
2乗とかあるとわかりにくい・・・。
このように書くと約分しやすいよ!
\[=\dfrac{3xxy4}{3xyy5}\]
で同じものを消して文字式の決まりに従って書こう!
\[=\dfrac{4x}{5y}\]
完成!
(3)nを自然数とするとき、3で割っても7で割っても1余る式として正しいものを次のア~エの中からひとつ選び、記号を書きなさい。
ア.6n+1
イ.14n+1
ウ.10n+1
エ.21n+1
3で割って1余る数は、3の倍数に1をたしたもの。式で表すと【(3の倍数)+1】
7で割って1余る数も、7の倍数に1をたしたもの。式で表すと【(7の倍数)+1】
両方で満たすようにするには
【(3の倍数でもあり7の倍数でもある)+1】
となります。
よって上の選択肢からこの条件に当てはまるのは21だから答えはエになるよ。
難しいコトバだと最小公倍数を求めればいいってことになるけど、上の考え方で全然OK!
もとの式にそのまま代入しても、もちろんできるけど、計算ミスが起こりやすくなるよ。
因数分解を使ってもとの式を簡単にしてから代入するのがおすすめ!
\[x^2-xy=x(x-y)\]
ここに\(xとy\)をそれぞれ代入!
必ずかっこをつけて代入しよう!
\[=(1+\sqrt{3})(1+\sqrt{3}-(1-\sqrt{3}))\]
うしろのかっこからひとつずつはずしていこう!
\[=(1+\sqrt{3})(1+\sqrt{3}-1+\sqrt{3})\]
さらにうしろのかっこを計算!
\[=(1+\sqrt{3})2\sqrt{3}\]
うしろの\(2\sqrt{3}\)を前のかっこの両方にかける。
\[=1×2\sqrt{3}+\sqrt{3}×2\sqrt{3}\]
\(2\sqrt{3}\)は分かりやすく書くと\(2×\sqrt{3}\)だから
\[=1×2×\sqrt{3}+2×\sqrt{3}×\sqrt{3}\]
\[=2\sqrt{3}+2×3\]
\[=2\sqrt{3}+6\]
これで終了!答えは\(6+2\sqrt{3}\)でもOK!
問題に解きなさい。って書いてあれば全部の項を同じ数で割ってOK!
問題に計算しなさい。って書いてあったら共通因数でくくりだそう!
ここでは解きなさいって書いてあるから、左辺の数字はすべて2の倍数なので2で割ります。
\(x^2\)の前の数字(係数)で割れることが多いよ。\[2x^2-6x-8=0\]
\[x^2-3x-4=0\]
\(x^2\)の前の数字(係数)がなくなったら
たして-3、かけて-4っていう和と積の因数分解の公式で解けることがほとんど。
できなかったら、解の公式を使おう!
今回は、-4と1でたして-3、かけて‐4になるから因数分解!
\[(x-4)(x+1)=0\]
ここまでくればもう解けたも同然!
\[(x-4)=0 または (x+1)=0\]
それぞれ移項して\(x=\)の形にすれば完成!
\[x=4,-1\]
(6)現在、父が42歳、子は12歳です。
父の年齢が子の年齢の2倍になるのは何年後か答えなさい。
父の年齢=子の年齢の2倍になると考えて、父と子の年齢を\(x\)を使って表そう。
\(x\)年後の父の年齢は今42歳だから、\((42+x)\)歳だね。
同様に\(x\)年後の子の年齢は今12歳だから\((12+x\))歳になるよ。
これを上の式に入れると
\[(42+x)=(12+x)×2\]
文字式の決まりに従って表すと
\[(42+x)=2(12+x)\]
あとは解く!まず右辺のかっこから
\[42+x=24+2x\]
文字を左に移項して
\[42+x-2x=24\]
今度は数字を右側に移項するよ。
\[x-2x=24-42\]
それぞれ計算して解こう!
\[-x=-18\]
\[x=18\]
答えはしっかり書こう!
★18年後
移項するときはひとつずつ丁寧にやっていくとミスが少なくなるよ!
(7)下の図の角度xを求めなさい。
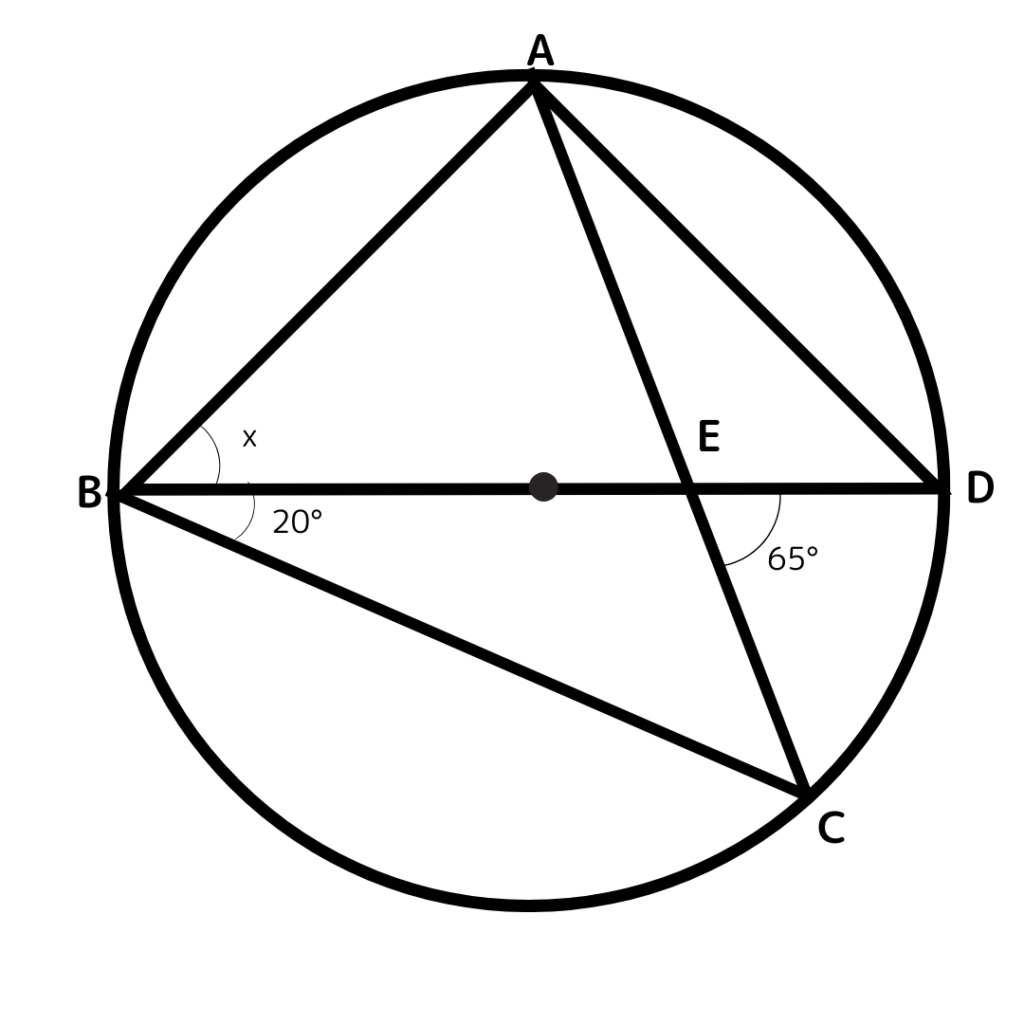
角度の計算はわかるところの角度をひとつずつ図に書き込んでいこう!
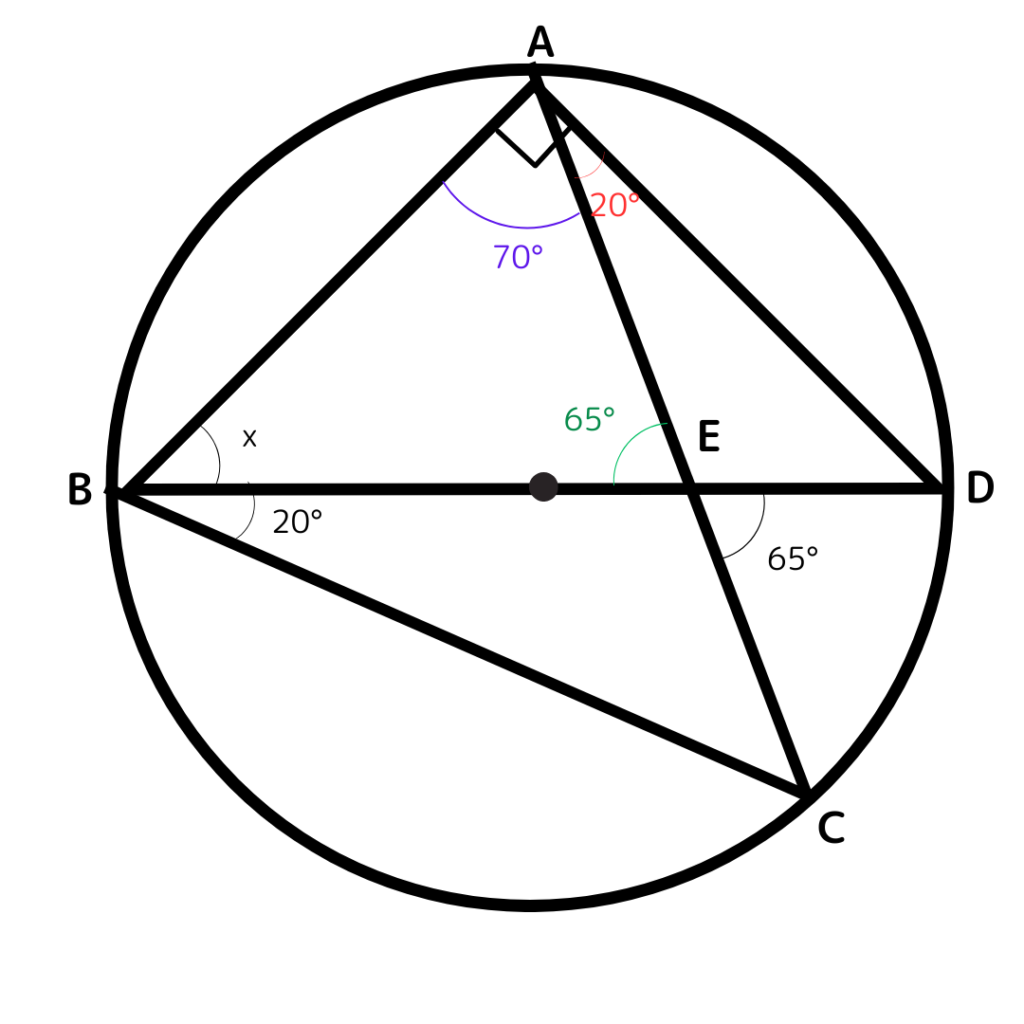
①対頂角が見える(緑の角度)
②円周角が見える
直径の円周角は90°
弧CDの円周角で20°(赤い角度)
ここまでは図から分かるよ。
ここから計算!
青い角度:90°ー20°=70°
角X:三角形ABEで内角の和から計算できるよ。
180°ー70°-65°=45°
よって45°
円周角は図形を回してみていろいろな方向から見てみると見つけやすいかも!
なかなか慣れてこないと難しいから何回もやってみるといいよ!
(8)長方形ABCDの頂点CをBD上の点Pに重なるように折ったときの折り目を作図しなさい。ただし、作図に用いた線は消さないこと。
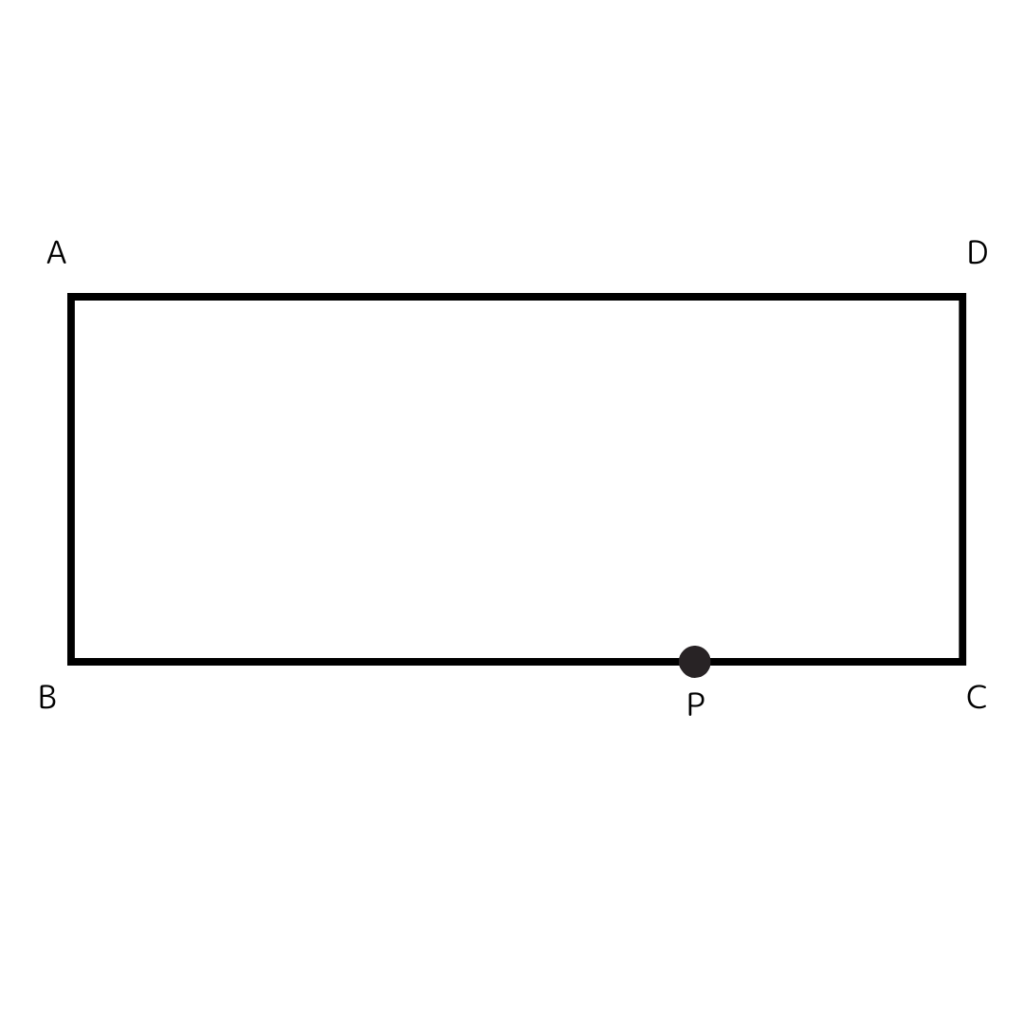
実際に紙を折って頂点Dを点Pに実際に重ねてみるといいよ。
そうすると、折り目は線分DPの中点(ちょうど真ん中の点)を通らないといけない。そうじゃないとDとPが重なることはないからね。
つまり、線分DPの垂直二等分線を作図すると折り目になるよ。
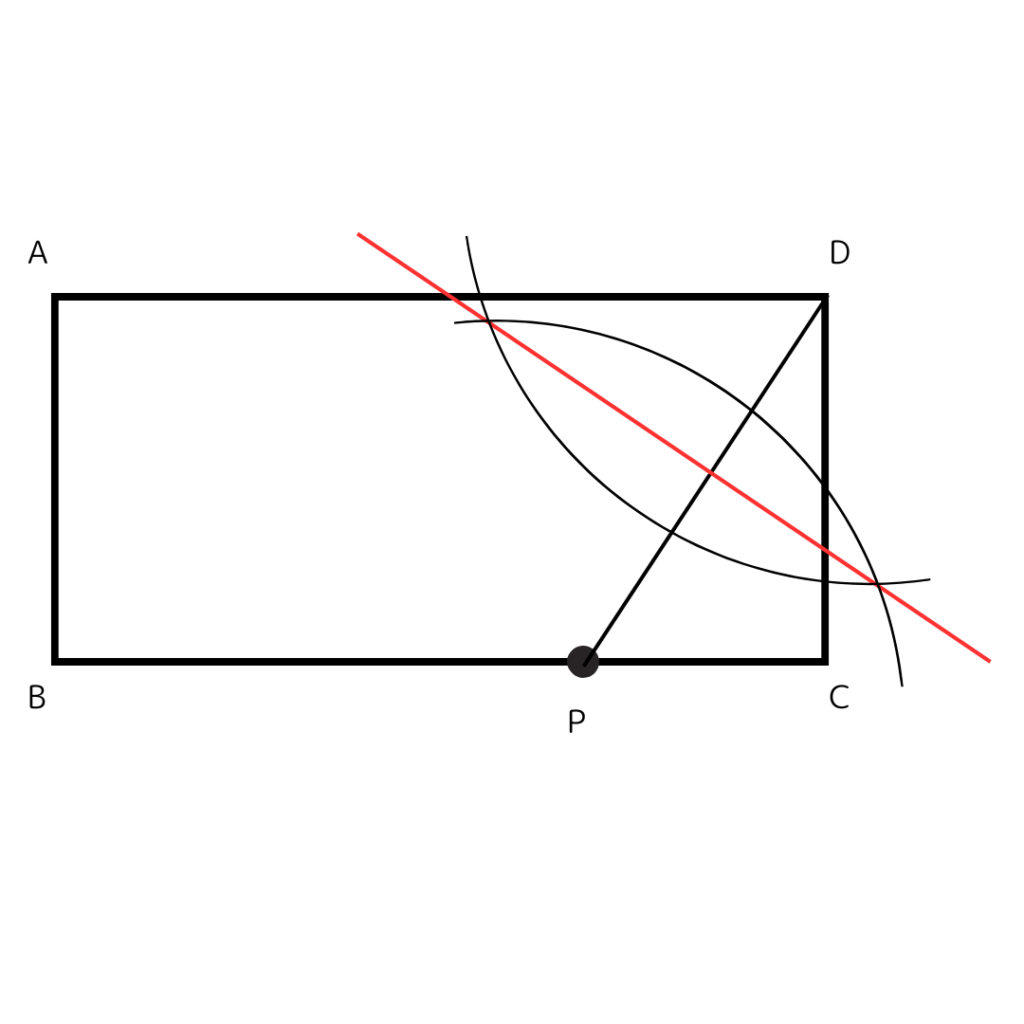
作図はこんな感じ。
そしてこれが答えだね。
(9)1.次の図のグラフ①のⅹの変域が-2≦ⅹ≦3のときのyの変域を求めなさい。
2.次の図のグラフ①と②のxの変域が-2≦ⅹ≦3のときの変化の割合について正しいものを次のア~ウから選びなさい。
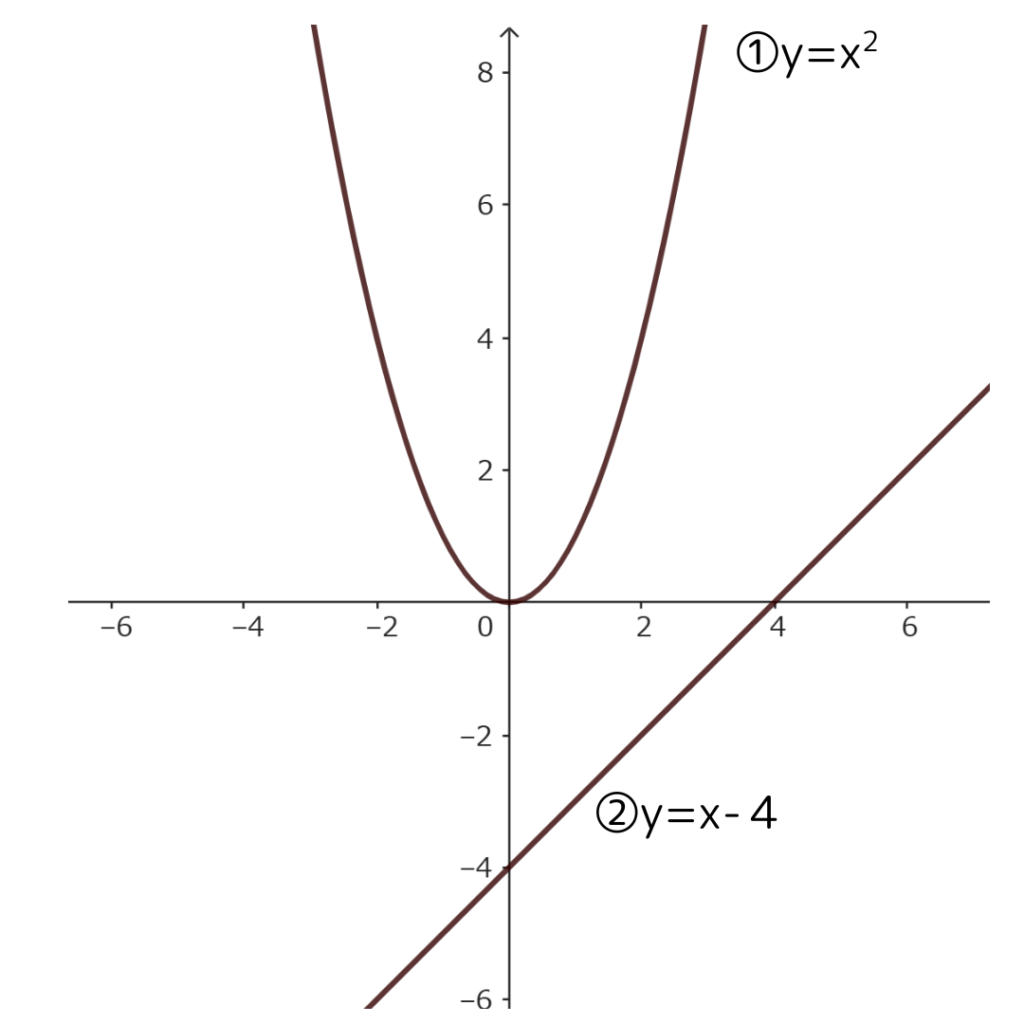
まずは1.から。
変域と言われたらまずは式に代入してもう一方の値を求めることが基本だね。
ではやってみよう!
\(x=3\)のとき、\(y=3^2\)だから \(y=9\)
一次関数ならこれでOK。
ただ\(y=ax^2\)はそうじゃないんだよね。 下の図をみてみよう。
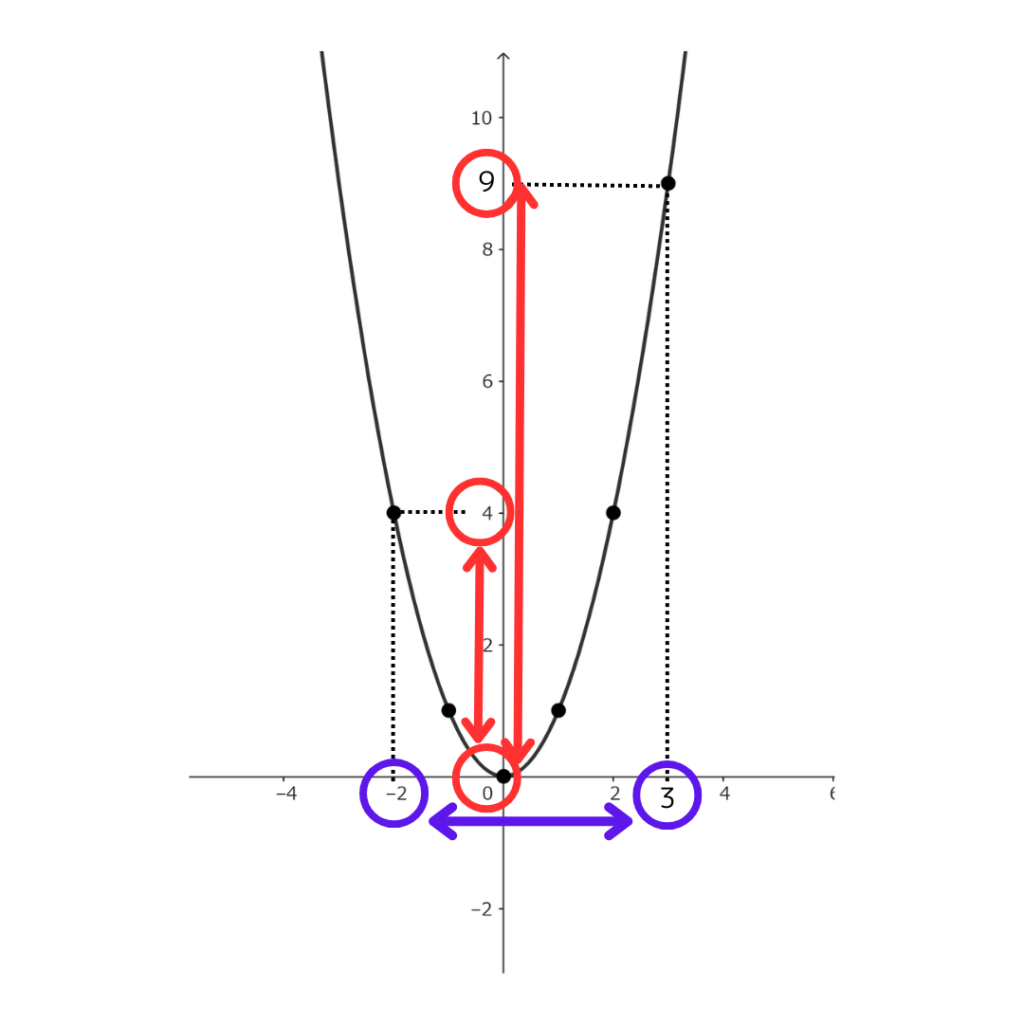
\(x=3\)のとき、\(y=9\)だよね。
でも\(x\)は-2から3までは動けるんだよ。
動いていくと\(y\)の値は減っていくのが分かる。
つまり一番小さい\(y\)の値は 0\((x=0\)のとき)
一番大きい\(y\)の値は 9\((x=3\)のとき)。
よって答えは\[0≦y≦9\]
グラフを見ながら考えるといいね!
次に2.だね。
まず、一次関数と\(y=ax^2\)の変化の割合は違うものって思うこと。\(y=ax^2\)は、\(xがpからq\)まで増加するときの変化の割合は\[a(p+q)\]で求められるよ。
なので、\[1(-2+3)=1\]
一次関数は式ができてると見るだけ。計算いらず。
\(y=ax+b\)の\(a\)が変化の割合だよ。
つまり、\(a=1\)だから変化の割合は 1。
\[よって答えは、ウ\]
(10)中の見えない箱のなかに1、2、3、4、5と書かれた5枚のカードがある。
その中から同時に2枚のカードを2枚取り出すとき、2枚に書かれた数字の積が奇数になる確率を求めなさい。
ただし、どのカードが取り出されることも同様に確からしいとする。

はい。確率の問題。
まず確認すること。
【2枚順番に取り出して並べる】→順番が関係するから全部の通りも多くなるよ。(1と2、2と1は違うもの)
【同時に2枚取り出す】→順番は関係ないので全部の通りも少なくなるよ。(1と2、2と1は同じもの)
これが確認できたら樹形図ですべての組み合わせを書き出そう!
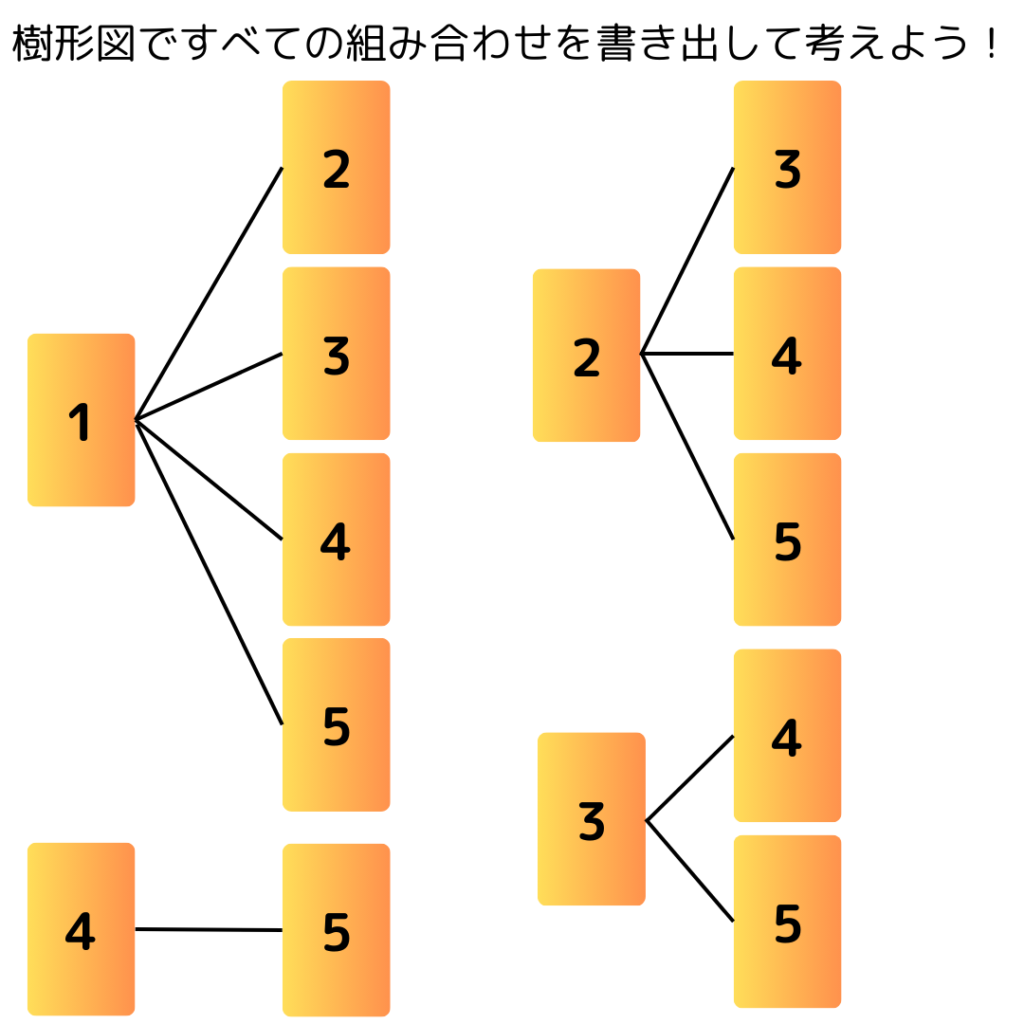
ここから積が奇数になるものを選び出そう!
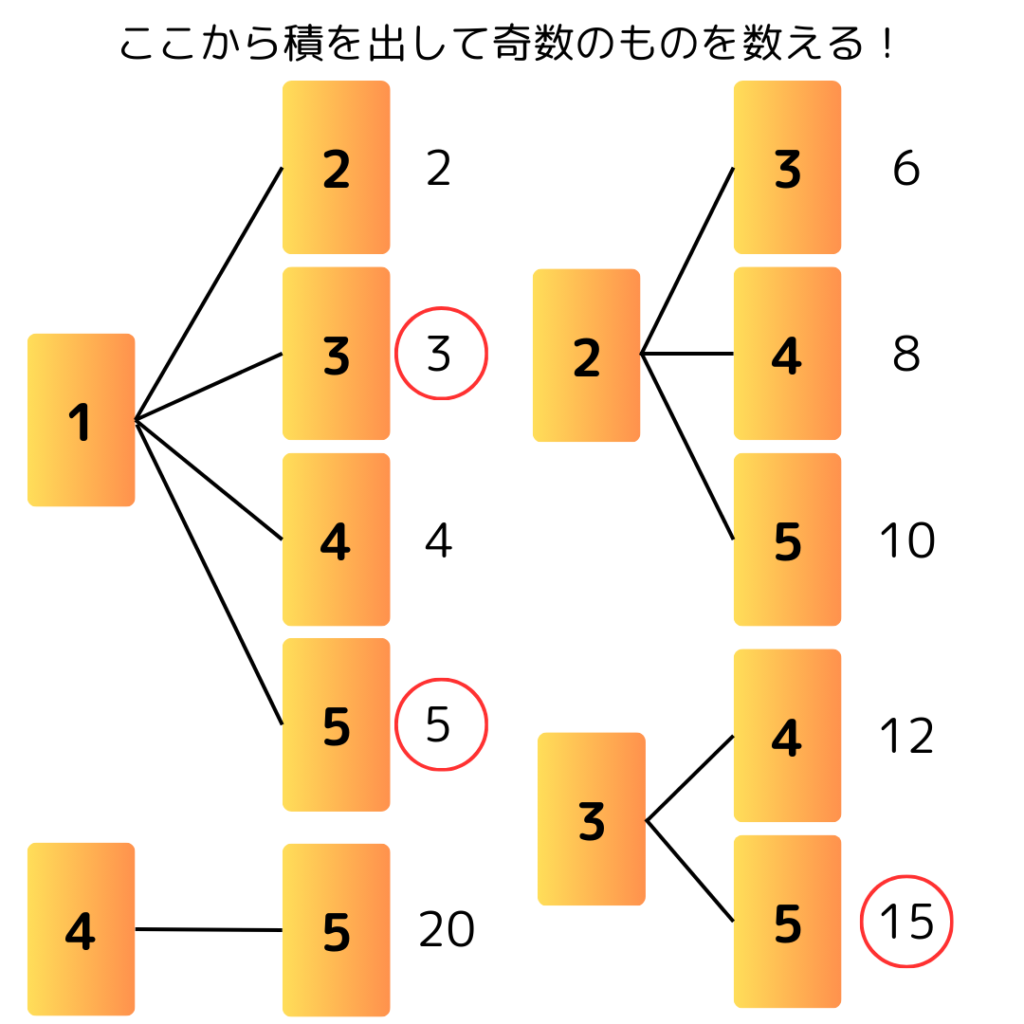
その中で積が奇数になるのは3通り。
よって答えは、\[\displaystyle \frac{3}{10}\]
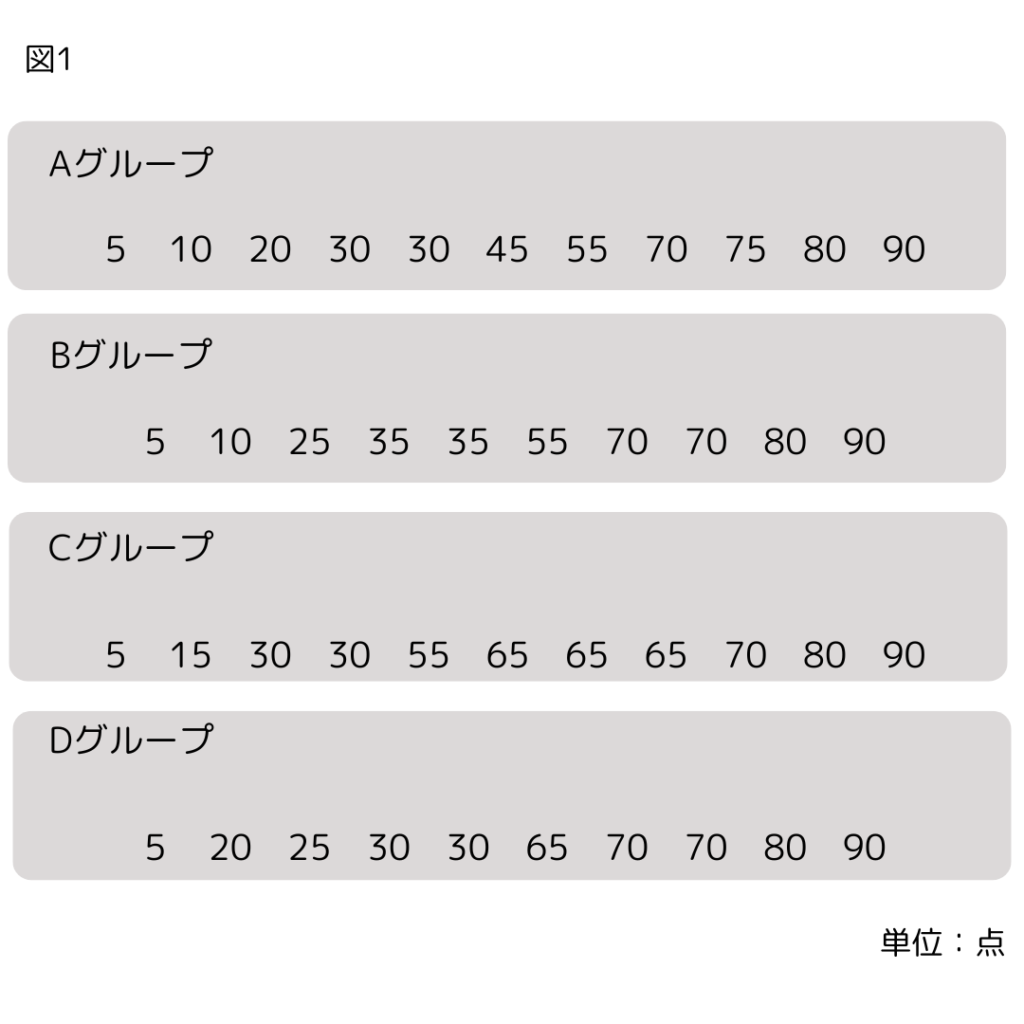
(11)図1は1問5点配点で100点満点のテスト結果のグループ別データである。
図2の箱ひげ図になるグループを2つ選びなさい。
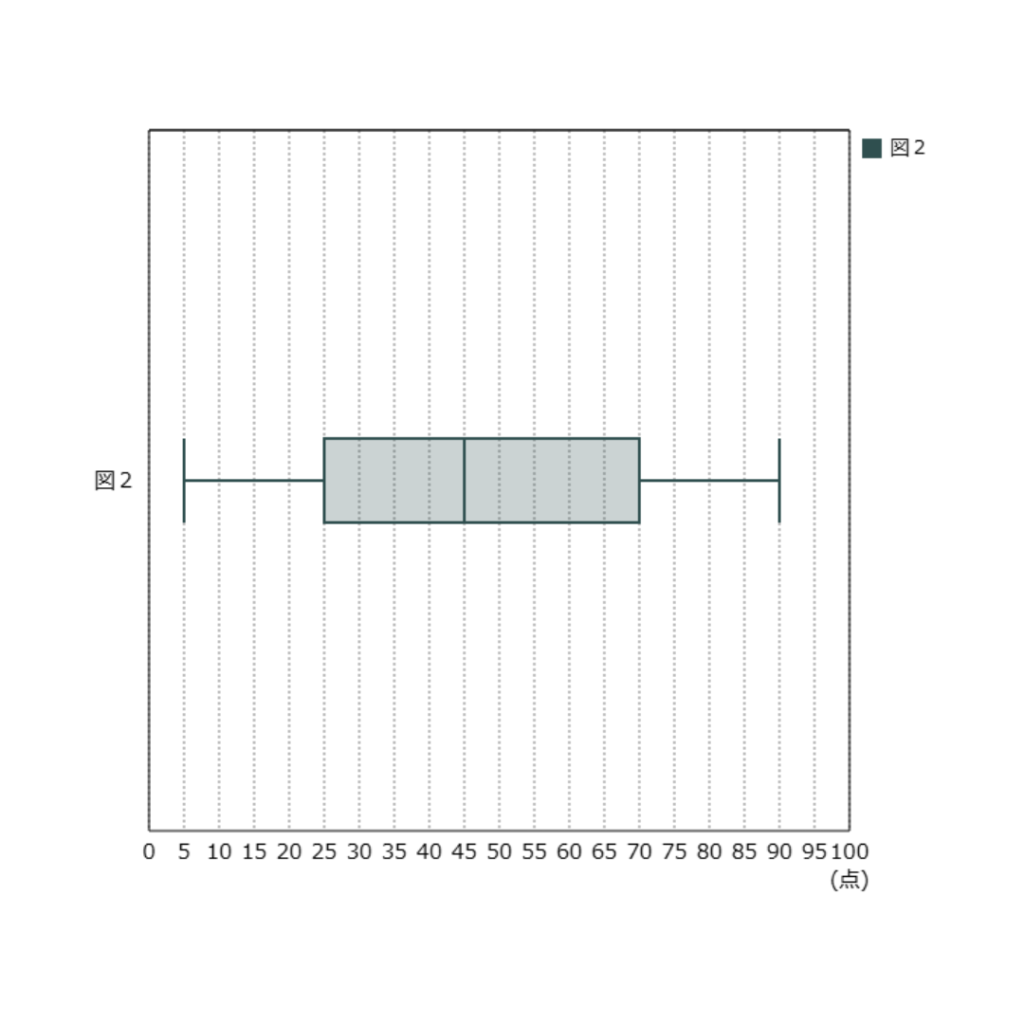
箱ひげ図の詳しい書き方はここにあるよ。
各グループの箱ひげ図を書くと以下の通り。
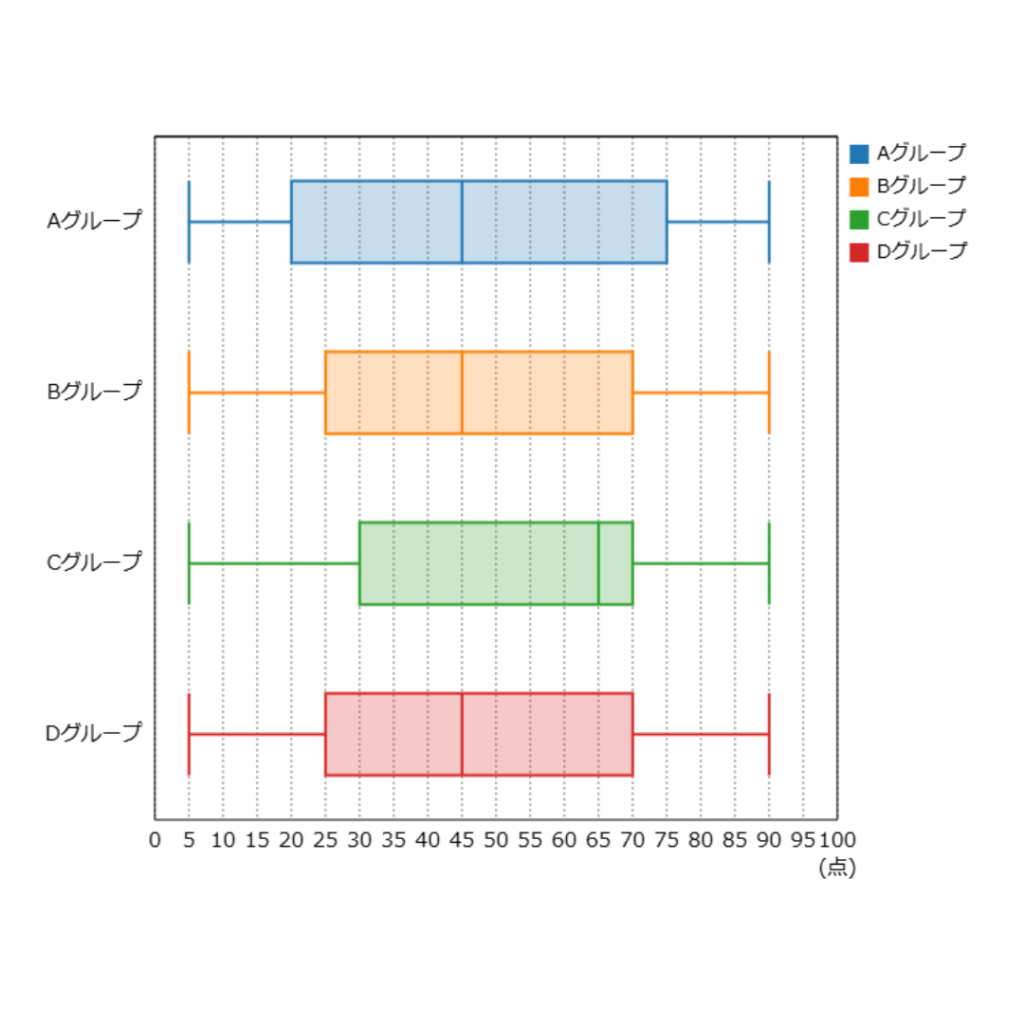
よって答えはBグループとDグループ。
箱ひげ図とヒストグラムの問題もよく出るから、しっかり図から情報を読み取れるようにしておこう。
実際の長野県の公立高校の入試の問1もこんな感じ。
ここは繰り返しやると点数がしっかりついてくるよ!
ひとりじゃできないなってときは一緒にやろう!
こちらから問い合わせてね。








