【青木島校】2学期期末テスト予想問題:中2数学

【問題】図の直角三角形ABCで、点PはAを出発して、毎秒2秒の速さで、辺上Bを通ってCまで動く。
点PがAを出発してからⅹ秒後の△APCの面積をy㎠とするとき、次の問いに答えなさい。

\(xとyの関係を表すグラフをかきなさい。\)

はい。動点の問題です。
その名のとおり点が動いていく問題だね。
これができると何に役立つのでしょう?
ひなさん。どうぞ!
う——ん…。
全然思い浮かばない…。
点が動いていることなんてほぼない気がします。


そうだよね!
一次関数は結構身近なところにあるんだけど、動点だと…。
物理や工学の基礎、経済や金融のほうに少し関係してくるかな。
動きを追っていくって大事な部分だからしっかり確認しておきましょう。
日常生活で使ってるけど、いざって言われるとなかなかピンとこないものも多いと思うよ。
さあ、問題進めよう。
まずは、問題文から、点Pがどこから
スタートするのかと動く速さを読み取ってみよう!
はい!
点PのスタートはA点です。
毎秒2cmだから1秒間に2cmずつ動くってことだね。


ちなみに…。
1秒間に2cmって…
めっちゃゆっくりだからね。
植物の成長とかカタツムリの移動とか。
あんまり目にする機会ないかもね。
1時間に72mしか動かないから。
そうなんだね。
秒速とかも時速にしてみたりすると
ちょっと分かりやすくなるかもね。
50mを6秒で走れば秒速は約8.3mだし。
問題文の速さって相当遅いよね。
問題もちょっと考えると新しい視点が
出てくるよね。


そうそう。とっても大事なことだよ。
気になったことは調べてみよう!
では、問題に戻りましょう。
点Pは、辺上をBを通ってCまで動く。
つまり、A→B→Cの順に通って進んでいきます。
動点はここがポイントです!
最初がグラフをかく問題だから、グラフをもとに考えてこっか。
グラフをかくときとかは、何かが変化するところに着目するといいって言ってたよね?
進行方向が変わるとか、進む速さが変わるとか。
動点はだいたい頂点で何かが変わるよね?


そうだね。
では頂点につく時間とそのときの△APCの面積を考えてメモっておきましょう!
ひなさん、Let’s Try!
おー了解!
\(x\)は点PがAを出発してからの時間で単位は秒。\(y\)は△APCの面積で単位は\(㎠\)。
ちなみに三角形の面積は
\(\frac{1}{2}\)×底辺×高さで求めれるよ。


はい!おっけーです!
では、順番にAから秒数(ⅹ秒)と△APCの面積(y㎠)から考えていきましょう!
はいよっと。
Aは点Pのスタート地点だから…\(x\)は0秒で、\(y\)は三角形にならないから\(0㎠\)かな?


はい、正解!
せっかく出したから、どこかにメモっておこう。
ではでは、AからBまでは何秒かかる?
辺ABが8㎝だから、8秒じゃないかな?


ぶっぶー。
問題よく読まないとこうなるって手本だね。
はい、ひなさん。もう一度確認するよ。
点Pって1秒間に何cm進むの?
えっ?うんっ?
あ!1秒間に2cmだ…しまった。
なので8÷2=4
つまり4秒ですね。


そう、正解!
みんなよく間違えるところだよ。
点Pの動く速さにしっかりしるしをつけておこう。ここは注意が必要なところ。
何事も経験が大切!
では、Bに点Pがあるときの\(y\)はいくつになるでしょう?ひなさん、遠慮しないでどうぞ。
めっちゃ確認しないとダメですね…
点PがBにあるときはこんな感じの三角形だね。

そうすると
\[\frac{1}{2}×8×6=24\]
点Bにいるときは24㎠だね。


いい感じ!
よし!もう一息だね。
じゃあ、ラスト!点PがCにあるときの\(xとy\)はどうでしょう?
さあさあ、どうかな?
きっとこうでしょう!
\(x\)は辺BCが6cmだから、6÷2=3で3秒。点PはAから進み続けているので、辺ABでかかった時間と合わせると
4+3=7だから\(x\)は7秒だね。


正解!考え方もばっちり!
\(y\)もいっちゃおう。お願いします。
いままでの流れで考えると…
うんっ?
三角形ができないから0㎠ってことだよね?


そうそう!
今までの部分を表でまとめるとこうなるよ。

これをもとにグラフをかこう!
表の3つの\(xとy\)の組み合わせをグラフで取ればいいよ。
一次関数の利用は、縦軸と横軸のひとメモリの大きさが違うことが多いから。
しっかり確認しといてね。
あっ!
縦軸のひとメモリが2になっている!
これをつないでっと。
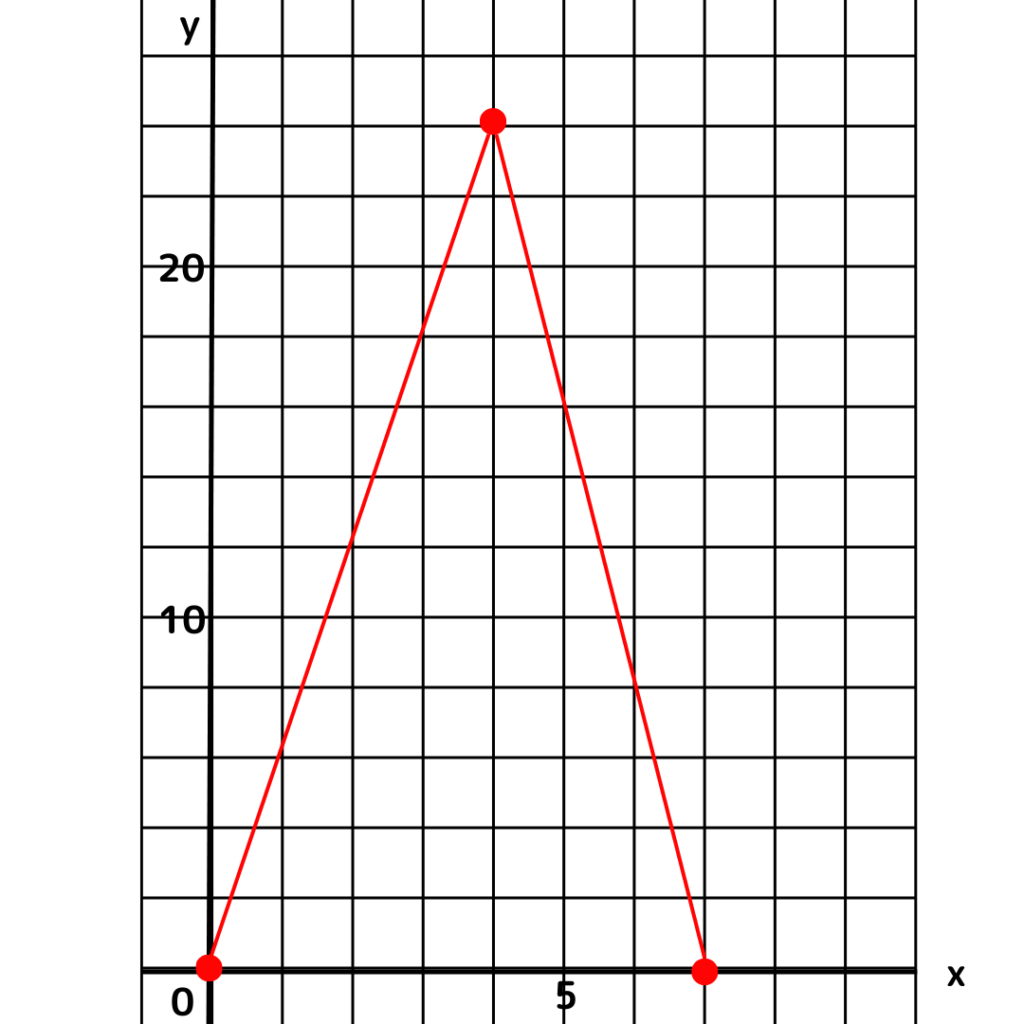
これで完成!
割とすっといけたから、よかったよ。

\(xとyの関係を表す式とxの変域を求めなさい。\)

OK!
さっきの表をもとにしていこう!
それと\(x\)の変域だから、BC上を点Pの動いている秒数ってことだね。
さっき作った表を確認してみよう!
BからCまでの間だから、4秒から7秒です。


そうですね。
つまり、4秒以上7秒以下ですね。これが\(x\)がとれる時間の範囲だね。
これで変域を表してみよう!
\[4≦x≦7\]ですね。


その通り!いいですね。
次は式を考えてみよう。
変域が分かっていると、さっきのグラフのどの直線と対応してるかが分かるね。
横軸が4から7のところにある直線だね。

そうすると
\((4,24)、(7,0)\)を通る右側の直線でいいよね?直線の一部分しか見えてないけど、それを伸ばしていくと…。
\(y軸\)とはどうみても原点で交わらないから、一次関数の式だね。
だから式の形は、\(y=ax+b\)で求めればいいね!


いいね!その通り!
直線の一部しか見えてないときは、自分で直線伸ばしてみよう!
そうすると切片が0かどうか見た目でわかるよ。
0ではなければ一次関数だって判断してOK。
では式を求めてみよう。
式を求めるやり方はここから見れるよ!
はーい!
2点を通るパターンだね。
\((4,24)、(7,0)\)を通るから、傾き\(a\)を求めるか。\[a=\frac{0-24}{7-4}=-8\]
\[\large{a=-8}\] だね。
次に、この\(a=-8\)を\(y=ax+b\)に代入するっと。
\[\large{y=-8x+b}\]
ここに\((7,0)\)を代入して、\[0=-8×7+b\]
あとは解いて…
\[-56+b=0\] \[b=56\]
★よって答えは \(\large{y=-8x+56(4≦x≦7)}\)


うーん!すばらしすぎる‼
ちなみに一次関数の式の求め方は連立方程式を使うこともできるよ。
連立方程式を使った式の求め方はここにあるよ。
どちらもできれば、問題に合わせて自分のやりやすいほうでできるから、計算ミスも少なくなるよ。
よし。やっと最後…長かった…。
問題には
\(△APCの面積が△ABCの面積の\frac{1}{2}になるのは、\)って書いてある。
これは△APCの面積が△ABCの半分になるってことでいいのかな?


そういう風に読み取れるね。
この問題文に当てはまるときの△APCの面積はいくつでしょう?
はい。ひなさん。
じゃあ、まず△ABCの面積を出そう。
△ABCの面積=\(\frac{1}{2}×8×6=24\)あ、これさっき計算したわ。
ま、確かめだと思えば無駄な計算じゃないね。
で、この半分だから、△APCの面積が12㎠ということだね。


OK!
そしたらグラフを有効活用しよう!
yってなんだったっけ?
yは△APCの面積だから、y=12ってことだね。
よくわからないけど、グラフにy=12をかきこんでみるとなにか分かりそうだね。
ちょっとやってみよう。
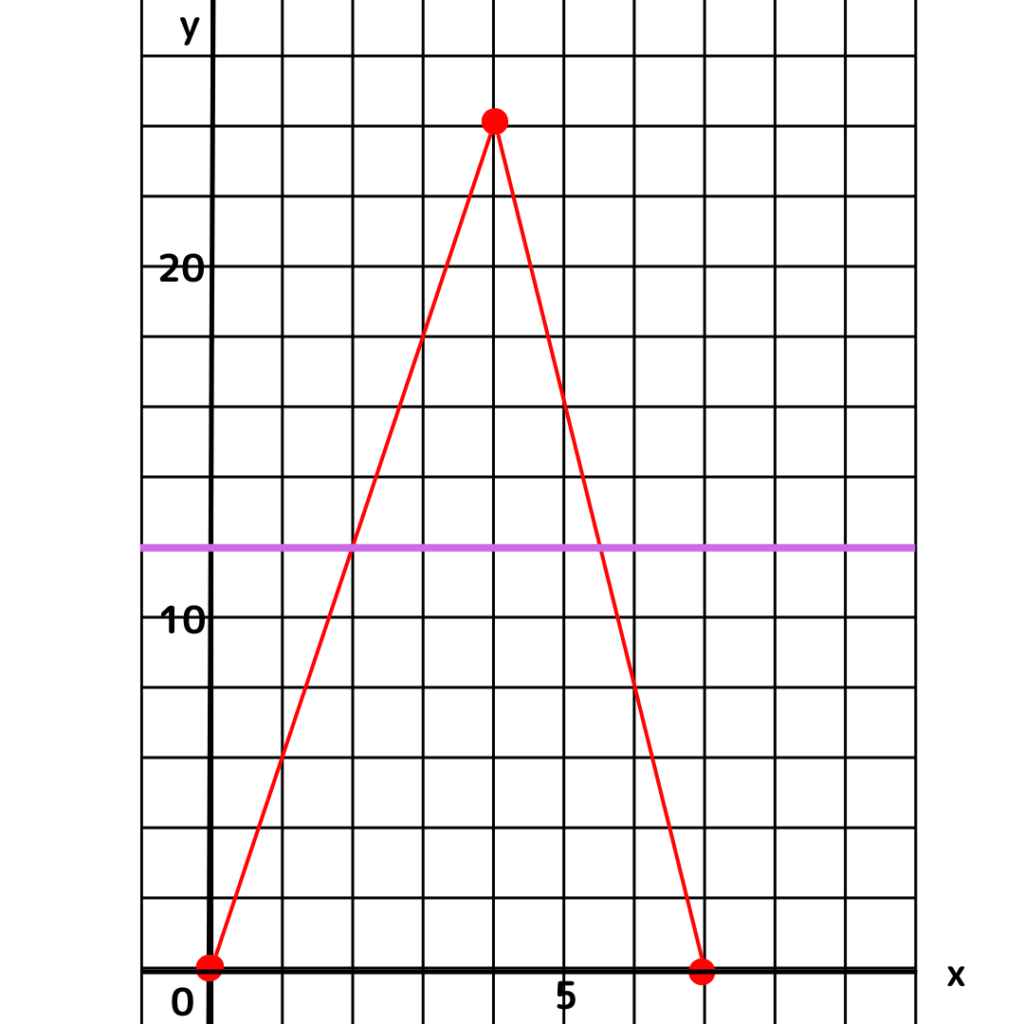
お!赤いグラフと2点で交わってるよ!
しかも1コはちゃんとした点で交わってる!
もう1コの点は、うーん。よくわからない…。


いい感じだね!
よくわからない1コは、たしか前の問題で直線の式が出してあったはずだね。
それを使ってみるといいんじゃないかな。
しっかりした点ではないので、もちろん整数では出てこないから、計算しっかり注意しながらやってみよう!
こんな感じで前の問題の答え使う問題も多いからね。
さまよいはじめたら、そこを思い出してみよう!
おおっ!そういうことか!
では、やってみよう!
では、\(y=-8x+56\)に\(y=12\)を代入してみます。さきに左辺と右辺を入れ替えて、
\[-8x+56=12\]
\[-8x=12-56\]
\[-8x=-44\]
\[x=\frac{11}{2}\]
これでもう1コの秒数もでました。
★よって答えは、\(2秒後と\displaystyle\frac{11}{2}\)秒後です!

Exactly!
たまには英語しゃべらないと忘れちゃうからね。
答えが出たら、グラフをもう一度確認しよう。
グラフの点のポイントと出た答えが違ったら違うからね。
動点の問題のポイントは図形の頂点にきたときの時間と図形の面積を把握すること。
これができるだけで、だいぶ解ける問題増えてくると思うよ。
面積出したい図形をかいて、その面積をしっかり出してみよう。
点の動く速さや図形のパターンでいっぱい問題は作れちゃうから、いろいろな問題で慣れておきましょう!
今回はこれで終了。








