【青木島校】2学期中間テスト予想問題：中２数学　

問題その1

ある遊園地の入園料は、おとな2人・こども1人で4500円、おとな4人とこども3人で9900円である。

おとな1人の入園料を\(x\)人、こども1人の入園料を\(y\)人として次の問いに答えなさい。 ❶文章中の黄色の部分と緑の部分のふた通りの買い方と、その代金の関係から\(x、y\)について次のような連立方程式をつくった。㋐、㋑にあてはまる数、または式を書き入れて、連立方程式を完成させなさい。 \begin{eqnarray} \left\{ \begin{array}{l} 2x + y & = & ㋐ \\ ㋑ & = & 9900 \end{array} \right. \end{eqnarray}

❷つくった連立方程式を解いて、おとな1人とこども1人の入園料をそれぞれ求めなさい。

この暑い中で遊園地！
まずは熱中症対策をバッチリしていこう！

この問題はきっと、ある家族で行くとこうなる・別の家族だとこうなるっていうのを集計したんだろうね。入園料の支払いは合計額だけ出てて、内訳がない領収書たっだ可能性が高い。
実際のところ入園料なんかスマホで調べればいいじゃん！って思います。
まあ考えなさいっていう問題だからしかたないけど。
スマホにない情報もいっぱい社会にはあるから、スマホに頼るなってことかな。

では考えてみよっか！

もう\(x\)と\(y\)は指定されているし、問題文も短いね。

文字が２つだから連立方程式で考えよう！
問題からわかることは？
はい、Ｓさん！

はい！え…なんでしょう？ぼーっとしてました…

はい、はい。分かりました。
問題からわかることは、合計の入園料が2つわかっています。

いつもListen to meしておくこと！

まずは❶から。
では、それで方程式を2つ立ててみよう！

ここでアドバイス!
【代金の合計】は【おとな1人の入園料】×【おとなの人数】+【こども1人の入園料】×【こどもの人数】だね。

おとな2人とこども1人で4500円だから

\[2x+y=4500\]だね。

おとな4人とこども3人で9900円だから

\[4x+3y=9900\]だね。

だから、連立方程式は

\begin{eqnarray} \left\{ \begin{array}{l} 2x + y &= &4500 ・・・①\\ 4x + 3y& =&9900・・・② \end{array} \right. \end{eqnarray} ★よって㋐は4500円、㋑は\(4x+3y\)です！

That’ｓ correct！いい感じだよ。

では、次は❷だね。
それでは連立方程式を解いていこう！

解き方は覚えているかな？
そう。まずは文字の前の数（係数）あわせから。

どうすればいいのか覚えてる？

もちろん！

2つの方程式を何倍かずつすればいいよね

例えば①を4倍して②を2倍すれば\(x\)の前の数字が8になってそろえられるね。そしたら引き算っと。

OK！悪くない解答だね。間違いじゃないし。

ただ、計算が多くなればなるほどミスも多くなるよ！

もっと簡単に考えてみよう。
両方に何倍かしなくてもよさげじゃない？

えっ？うん…そうか！

さらに数字が小さいほうが計算ミスも少なくなるよね。ってことは・・・
①を2倍すればいいしない。

すばらしい考え方だね！
では、そのあとの考え方をみんなに教えてあげてくれる？

先生にそう言われるのならしかたないなあ。

では①×２をすると

\[4x+2y=9000・・・①’\]

そしたらひき算だけど、できるだけマイナスは出したくないから…②-①’をしよう。

\begin{eqnarray} 4x + 3y &= &9900 ・・・②\\ -)4x + 2y& =&9000・・・①’\\ y&=&900 \end{eqnarray} 次は\(y=900\)を一番簡単な式の①に代入して \begin{eqnarray} 2x+900&=&4500\\ 2x&=&4500-900\\ 2x&=&3600\\ x&=&1800 \end{eqnarray} よって\((x,y)=(1800,900)\)より

★おとな1人・1800円、こども1人・900円です！どうでしょう？

言うことなし！Sさんきっと先生になれるよ！

今日はあと2問あるから次の問題はSさんが先生になって進めてくれるっていうので！

じゃ次にいってみよう。

問題　その2

1周2.7㎞のランニングコースがある。健司くんはこのコースを最初は分速100ｍで走り、途中のベンチで5分間休憩したあと、分速150ｍで走ったところ1周するのに30分かかった。健司くんは分速100ｍで走った道のりと分速200ｍで走った道のりを求めるために次のような方程式をつくった。

\begin{eqnarray} \left\{ \begin{array}{l} 100x + 150y &= &2700\\ x +5+y& =&30 \end{array} \right. \end{eqnarray}

健司くんは何を文字で表し、どのような数量の関係から連立方程式をつくったのか説明しなさい。

では、ご指名されたので、やってみようと思います。
まず、文章問題は図や表などで、目から見える情報にすることが大事かな。
手を動かすことで、考えも整理されてくると思うんだけど。
先生どうかな？

That’ｓ a good way of thinking!

すごくいいこと、大事なことだね。
これをするかしないかでだいぶ変わるね。

では、Sさん続けてお願いします。

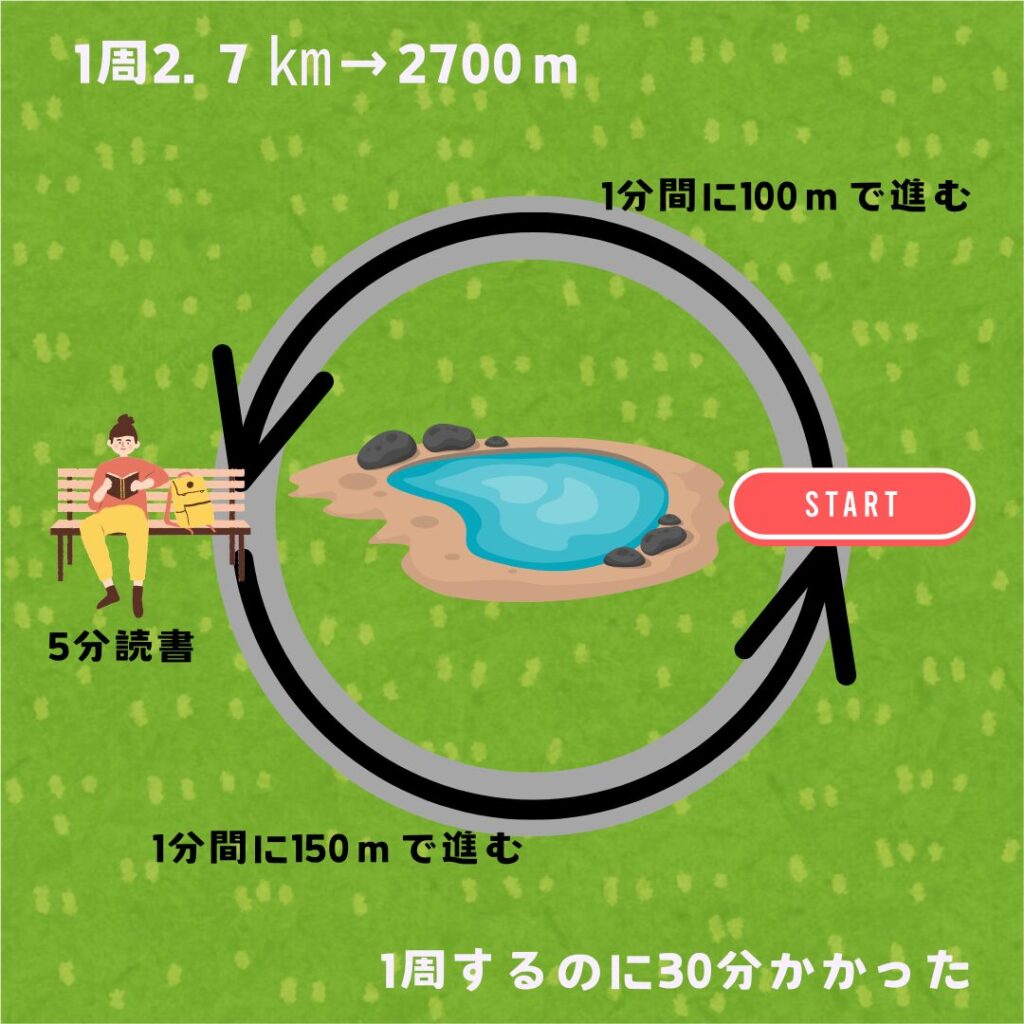
こんな感じに図にしてみました。

健司くんはランニング中に明日の英語の単語テストがあるのを思い出して休憩中に時間の有効活用をしようとしたと考えたので、整わない呼吸で休憩中は単語帳を音読しています。
ぼくもそういうときがあるからね。

とりあえず小数点は大嫌いなので、単位をかえて2.7㎞は2700ｍにしたよ。

でもこれだと少しわかりずらかったので、数直線にしました。
この図は出さなくてもよかったんだけど、せっかく時間かけてつくったから見てもらいたいです。

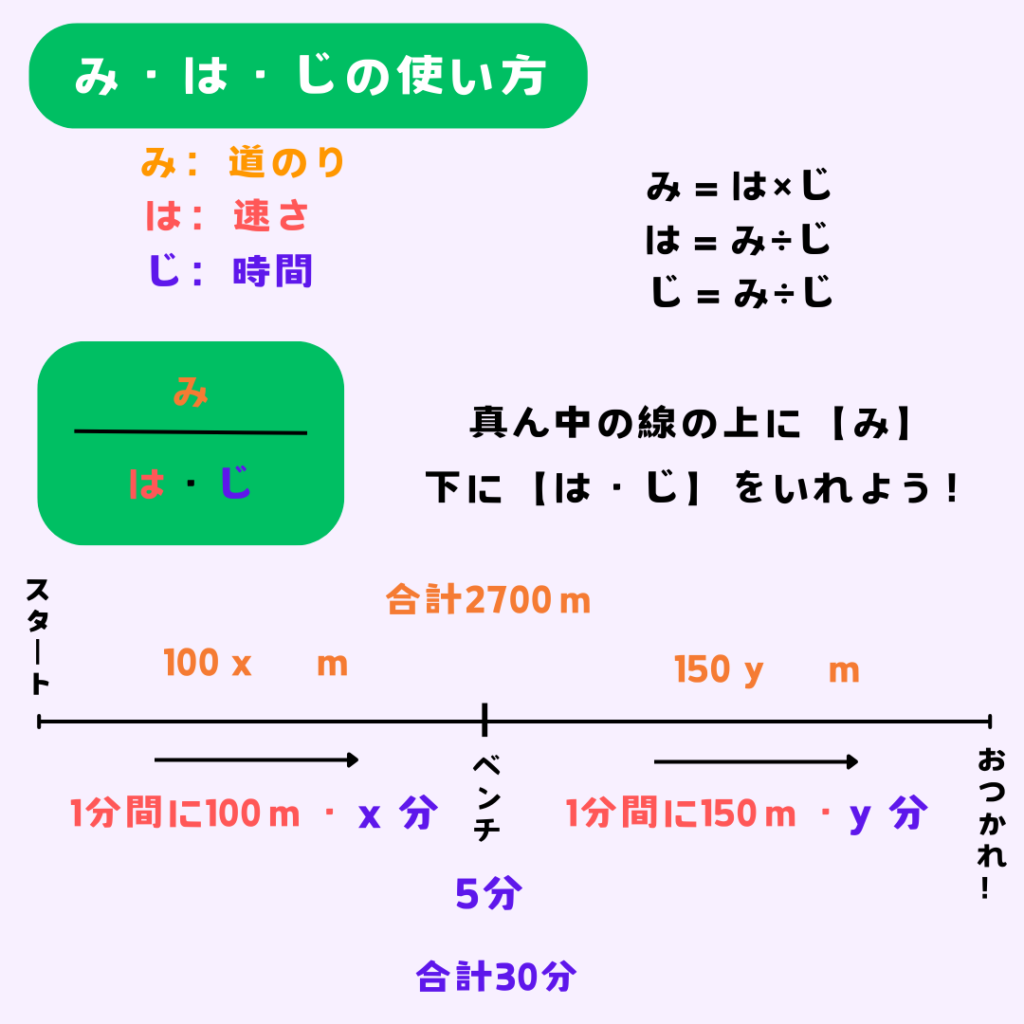
数直線であらわしたものだよ。

速さの問題だから【みはじ】も一緒にまとめてみたよ。問題では下の式のたし算した合計が［30］となっているので［時間の合計］だと判断できるかな。さらに［5］って記述もあるのでこれも［時間］だよね。以上から［ｘとｙは時間］じゃないかと仮定してみる。

そのあとで、上の式を見ると合計が2700ｍになっているから道のりの合計になっています。100ｘと100ｙとなっていることから、これは（速さ×時間）。
つまり、道のりを表しているので、こちらの確認でも［文字は時間］でよさそうです。

Amazing!!さすがの一言だね。いうことないよ。
速さの部分は【みはじ】をしっかり利用するとかなりできるようになります。
上の図はかなりまとまっているので参考に問題を解いてみるといいかも。

ここで少し解き方をまとめてみます。

\begin{eqnarray} \left\{ \begin{array}{l} 100x + 150y &= &2700・・・①\\ x +5+y& =&30・・・② \end{array} \right. \end{eqnarray}

①は(分速100ｍで走った道のり）+（分速150ｍで走った道のり）＝（走った道のりの合計）
②は(分速100ｍで走った時間）+（休憩時間）+（分速150ｍで走った時間）＝（かかった時間の合計）

となるよ。

まだ、問題の答えは出ていないね。
遠足といっしょ。最後（おうちに帰る）までで終了だし、ここまでだとせっかくの得点を失点してしまうからね。

じゃあ最後のおいしい部分はSさんどうぞ。

ありがとうございます。

★よって健司くんは、分速100ｍで走った時間を\(x分\)、分速150ｍで走った時間を\(y分\)とし、走った道のりの関係とかかった時間の関係から連立方程式をつくった。

という解答です。

Special Thanks!

はい、みなさん拍手！おつかれさまです。
ただ、今日はもうひとつ問題が待っています。
もうひとふんばりしまっしょい。

問題　その3

ある中学校の生徒数は男女あわせて530人である。そのうち男子の6％と女子の10％は合唱部に所属していて、その人数は43人である。
この中学校の男子と女子の生徒数をそれぞれ求めなさい。

はい。でた。よく出るやつ！割合の問題だね。

だいたい部活名はその先生の好みで決まっていると思います。推測だから違うかもしれないけど。
私だったら生物部にするね。こんなどうでもいいことでも、問題を解くだけではなく、いろいろなことを考えていくことってすごく重要だから。実際に生徒ともこんなこと話したりするし。

さあ、問題解いてみようか。

今回3回目の連立方程式です。
いままではもう文字で置いてくれてあったけど、今回は、まず何を文字で置くのか決めましょう。
分からない数量を探して文字にしよう。

はい。では合唱部のRさん！

やっぱり！そうくるよね…ご指名いただきありがとうございます。
分からないもの…問題で聞かれている数量でもいいって感じだったよね。確か。

なら男子の生徒の数を\(x\)人、女子の生徒の数を\(y\)人にします。

OK！そうだね！
では、次はしつこいけどまずは合計が分かっているものに着目！
合計は基本問題に書いてあるからあんまり考えすぎないように。

はい。合計が分かっているもの…【全校の生徒数】と【合唱部の人数】が書いてある！

どうでもいいけど、全校530人で合唱部は43人だって。
うちの学校は全校450人で合唱部は40人なんだけど、全校生徒のうちの合唱部ってどっちが多いんだろう？
うちの部活は出席率高いからいつもたくさんいるように見えるけどね！

そうそう。合計に関してはその２つでOKだね。

ちょっと、いまRさん、とてもいいこと言ってくれました。
全体の人数が違うときに大小を比べるられるようにするのが割合だね。
大切なところだから割合についてはもう少しあとで。

まずは割合を使っていない全校生徒の数で方程式をつくってみよう。

了解！

男子の生徒の数を\(x\)人で女子の生徒の数を\(y\)人だから、 \[x+y=530\]

ですね。

Exactly!いいね。

では次に合唱部の人数だね。
こっちは割合を使って表現されているね。

そもそも割合は全体に対するその部分の大きさの比率のことだね。
よく％が使われるね。

全体×割合でその実際の数量が計算できるよ。
ただ、％のままでは計算できないから、〇％だったら

【全体】×\(\displaystyle\frac{〇}{100}\)でOK！

そういうこと！ではやってみますね！

男子の生徒の数が\(x\)人で6％は\(\frac{6}{100}\)だから\[\displaystyle\frac{6}{100}x(人)\] 女子の生徒の数が\(y\)人で10％は\(\frac{10}{100}\)だから\[\displaystyle\frac{10}{100}y(人)\]

だね。合唱部の合計が43人だから

\[\displaystyle\frac{6}{100}x+\frac{10}{100}y=43\]

という式ができます。

Amazing!すばらしい！

今までのものをまとめるとこんな感じかな。

表を使うと理解しやすくなるよ。
私は表を使うのをおすすめしています。

いろいろなやり方があるから考えるのもひとつだし、考えたことはしっかり理解して定着できるようになるからこれもやってにるといいね。

Rさん、あとはお任せします！

はい！自信ないけどやってみます。
まずは２つ方程式ができたから、連立させると

\begin{eqnarray} \left\{ \begin{array}{l} x + y = 530・・・① \\ \displaystyle\frac{6}{100}x+\frac{10}{100}y=43・・・② \end{array} \right. \end{eqnarray}

うーん。②の式が分数だから分母にある100をかけてみるか。（②×100）

\[6x+10y=4300・・・②’\]

OK！右の43もちゃんと100倍されてるね。

次は…文字の前の数字（係数）をそろえるから6のほうが小さいけど、10のほうが計算が楽そう。
だから①×10します。

\[10x+10y=5300・・・①’\]

よし！ならマイナスは出てこないでほしいから…①’-②’をしよう。

\begin{eqnarray} 10x + 10y &=& 5300 \\ -)6x+10y&=&4300\\ 4x&=&100\\ x&=&250 \end{eqnarray} \(x=250\)だから一番簡単な①の式の\(x\)を250に置き換えて（代入して）そうすると答えは\((x,y)=(250,280)\)だから確かめをしてみて…うん。OK！

最後にしっかり答えを書くと、
★この解は問題にあっているので、男子250人、女子280人です。