【篠ノ井校】2学期中間テスト予想問題:中2数学

はるかさんは次の問題を考えている。
(問題)
\(yはx\)の一次関数で、そのグラフが2点\((-2,-6),(3,4)\)を通る直線であるとき、この一次関数の式を求めなさい。(1)はるかさんは、この(問題)を解くために次のように考えた。
【はるかさんの考え方】
①求める一次関数の式を\(y=ax+b\)として対応する2組の\(x,y\)の値をそれぞれ代入し、\(a、b\)についての連立方程式をつくる。 ②つくった連立方程式を解いて、この一次関数の式を求める。【はるかさんの考え方】の①にしたがって連立方程式をつくりなさい。ただし作った連立方程式を解く必要はない。

さあ、今回は関数だね。
みんなとてもイメージしにくいものだって思ってるけど、意外と身近なものも一次関数で表せるよ。
例えば、英単語の暗記した個数とか。実際に式にしてみよう!
では、Yさん、いま自分が覚えている英単語の数っていくつぐらいだと思う?
う-ん。わかんないな。ちょっと待って・・・。
今の時期だと、グーグルさんに聞いたら550語ぐらい覚えてないといけないらしいからそれぐらいじゃない?


OK!それぐらいかもね。自分で何か調べるのもとても大事なことだね。
では、いま550語覚えてるとして、1日10個ずつ新たに覚えるトライをしたとしよう。
そうすると15日後にYさんにインプットされているはずの英単語はいくつになる?
いま550語で10個ずつ15日だから、10×15で150個。
これをたして550+150=700。700語だね。


そのとおり!いまは15日後だったよね。
では20日後は10×20=200、200+550=750だね。
30日後は10×30=300、300+550=850というように計算できるね。
Yさん、ここまでで気づくことない?やさしいからヒントで色つけておいたけど。
でた!いつものやさしさアピール・・・。
うーんと。
1日10個だから10っていう数字と今までに覚えている単語数は変わるわけないからいつも550。
変わる数は日数だけだね。先生が赤で色つけしてくれたところ。


Good catch!いいね!
つまり【覚えた英単語の数】=【10】×【日数】+【550】となってるね。
★ここで、変わる数(変数)は【日数】と【覚えた英単語の数】になるので【日数】を\(x\)、【覚えた英単語の数】を\(y\)とすると、\(x\)日後に覚えた英単語の数\(y\)はどうなるかな?余裕っしょ!
さっきの式の【日数】を\(x\)、【覚えた英単語の数】を\(y\)に変え(代入す)ればいいから・・・ \[\large{y=10x+550}\] ってなるよ。あれ?なんとなく\(【y=ax+b】\)みたいになってるじゃん!これって一次関数だよね。


Exactly!その通り!
わりと遠い存在だと思われているけど、スマホ代や水道代、電気代なんかも一次関数で表せるよ。
考えてみることが大事だからね。複雑になっちゃうかもしれないけど、人生はトライがモットーのYさんまたやってみてね。
全然本題に入れないからおうちですみませんが、お願いします。
うん。時間あったらね。
絶対やるってお約束はできないけどさ。


OK!じゃあいこう。
いるよね。
こうやって余計な話してて授業進まなくなってテスト前すごい早さで進む先生。
わりとあるある。
今度こそ問題解くよ!
一次関数の式の求め方を考えましょうっていうことだよね。
そうっぽいね。
でもどうやったか忘れちゃった・・・。


OK!人間は忘れる生き物だからしかたない。何度もやって覚えよう。
ちゃんとYさんのためにまとめた資料作っておいたから。やっぱりやさしさが違うよね。

またきた!
やさしいひとは自分からやさしいって言わないもんだけどね。


それよく言われるやつ!でも言い続けるけどね!
はい。Yさん。問題はどっちのパターンかな?
ちょっと待って・・・。
\((x,y)\)が2コわかってるからパターン2だね。えーっと連立で解く?どうやったっけ?


As expected!いい発言だね。
そういうと思ってまとめておいたよ。
やっぱりやさしさが・・・。

分かった、分かった!しつこいな・・・。
だから彼女も・・・・・・・・・。こういうのよくないね。
先生ごめんなさい。


なに?よく言われすぎて全然気にならないから、Don’t Worry!
では、Yさん。
Let’s try solving this problem!
I can do it if I try!
まずは\((-2,-6)\)を\(ax+b=y\)に入れて\[-2a+b=-6\] 次に\((3,4)\)を\(ax+b=y\)に入れて\[3a+b=4\]★この2つを連立方程式にすればよいから
\begin{eqnarray} \left\{ \begin{array}{l} -2a + b = -6 \\ 3a + b = 4 \end{array} \right. \end{eqnarray}これが解答だね。


Good job!ありがとう。
みなさん、Yさんに拍手!
時間もないから次の問題にいこう。
(2)この(問題)についてさちさんとかずきくんの2人が以下のような会話をしている。
さちさんとかずきくんの会話
さちさん「この問題は、ほかの方法で解くことはできないのかな。」
かずきくん「実際に正確なグラフをかいて、グラフから切片と傾きを読み取れば、式は求められるね。」
さちさん「そうだね。でも、グラフ用紙がなければかけないね。」
かずきくん「正確なグラフがかけなくても、今までに学んだことを使えば解けるよ。」
さちさん「どんなふうに解けばいいの?」
かずきくん「それはね、【かずきくんの考えた解き方】」
かずきくんはどのような解き方を考えたのか、【かずきくんの考えた解き方】に適するかずきくんの考え方を書きなさい。
(3)【はるかさんの考え方】または【かずきくんの考え方】を用いて、この一次関数の式を求めなさい。また、求める過程も書きなさい。

はい。やっと(2)まできました。
ここも考え方の問題だね。
ここからはOさんにお付き合いいただきます。
Oさん、聞こえてますか?
はいはーい!聞こえてますよ!
さっきの解き方しか知らないんだけど…。困った。
先生、help me!


OK!
連立方程式で解いた方が考えることあんまりなくて楽なんだけど…
それ以外って言われているから、変化の割合(傾き)を先に求めようってやり方だね。
Oさん、説明してみよう!
Let’s take on the challenge!
Oh…Sorry. I can’t.
できそうでできない・・・。
ヒントくださいよ!


こんなこともあろうかと寝ずにまとめておいてよかったよ。
やっぱりやさしさしかないね。
じゃあこれ見て答えてみよう!

では、いかせていただきます。
★直線が通る2点の座標から、変化の割合(傾き)を求めます。
それを
次にどちらかの座標をこの式に代入すればbが求められます!
以上、ご清聴ありがとうございます。


Amazing!すばらしい!
2点を通るタイプの問題は両方で解けるようにしておいた方がいいよ!
最近は解き方が決められてきているから、対応できるようにしていこう。
じゃ、Oさん、あとは(3)だね。
ズバっと解いて目立ってちょうだい!
Thank you!
まずは【はるかさん】から。
★連立方程式を解きます。
bがそろっているのでそのままひき算します(①-②)
\begin{eqnarray} -2a + b &= & -6 \\ -)3a + b& = & 4\\ -5a & = & -10\\ a &= &2 \end{eqnarray} マイナスはいやだから\(a=2\)を②に代入します。 \begin{eqnarray} 3×2+b&=&4\\ 6+b&=&4\\ b&=&4-6\\ b&=&-2 \end{eqnarray} あとは\(y=ax+b\)に\(a=2,b=-2\)を代入して \[\large{y=2x-2}\]
つづいて【かずきくん】
★まず傾きを求めます。
2点(-2,-6)、(3,4)を通る直線の傾きは
これに計算が楽な方の(3,4)を代入します。
\begin{eqnarray} 2×3+b &= & 4 \\ 6 + b& = & 4\\ b & = & 4-6\\ b &= &-2 \end{eqnarray} あとは\(y=2x+b\)に\(b=-2\)を代入して \[\large{y=2x-2}\]

Cool!かっこいい!
Oさんに心からの拍手を。
yが左にあると計算ミスしやすいから最初からyを右においておくのがポイントだよ。
Oさん、Thank you!
では、今日はこれで終わり・・・ん、うそ!裏もある・・・。
もういやだけど、やってしまおう!
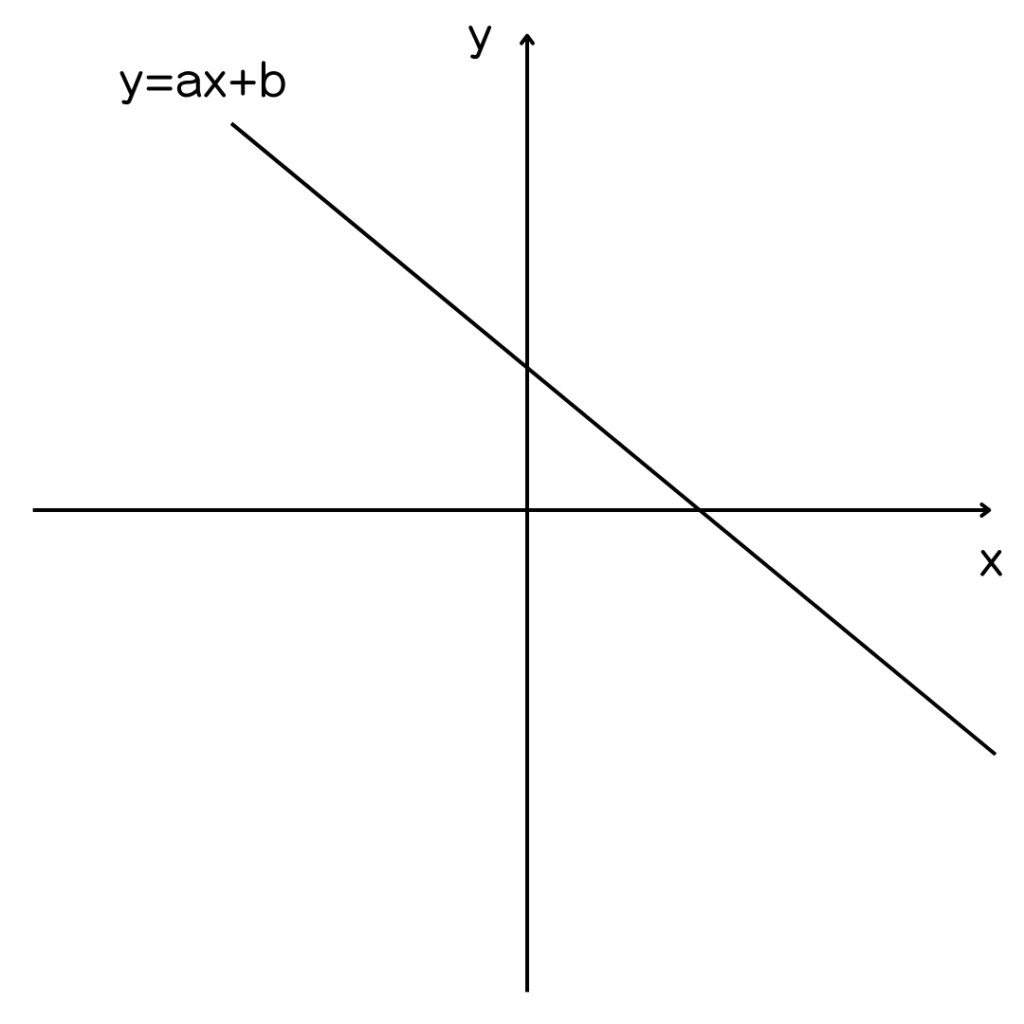
右の図のような関数y=ax+bのグラフがある。
このときa×bの値は正の数・負の数どちらになるか答えなさい。
また、そのわけを説明しなさい。

さあさあ!これで本当に最後です。今日は長い1日でした。
はい。グラフの問題だね。
a×bって書いてあるね。
では一次関数の式のaとbってなんだっけ?Yさんどうぞ!
また、あたし?
しょうがないな。頼られるのはきっといいことだよね。
確かさっきの資料だと…
aは傾き(変化の割合)、bは切片だよね。


Excellent!すごいじゃん!めっちゃいい感じ!なにもいうことない!
では、いまのグラフだと傾きと切片はそれぞれ正の数・負の数どっち?
は?え?そんなのわかるわけないじゃん!
グラフに数字もなんにも入っていないのに。
Teacher, say what?


そう思う?それがわかるんだな。
直線の場所と傾き方で正負の判断だけはできるよ。
やさしいteacherがみんなのためにつくりました。
見てください。
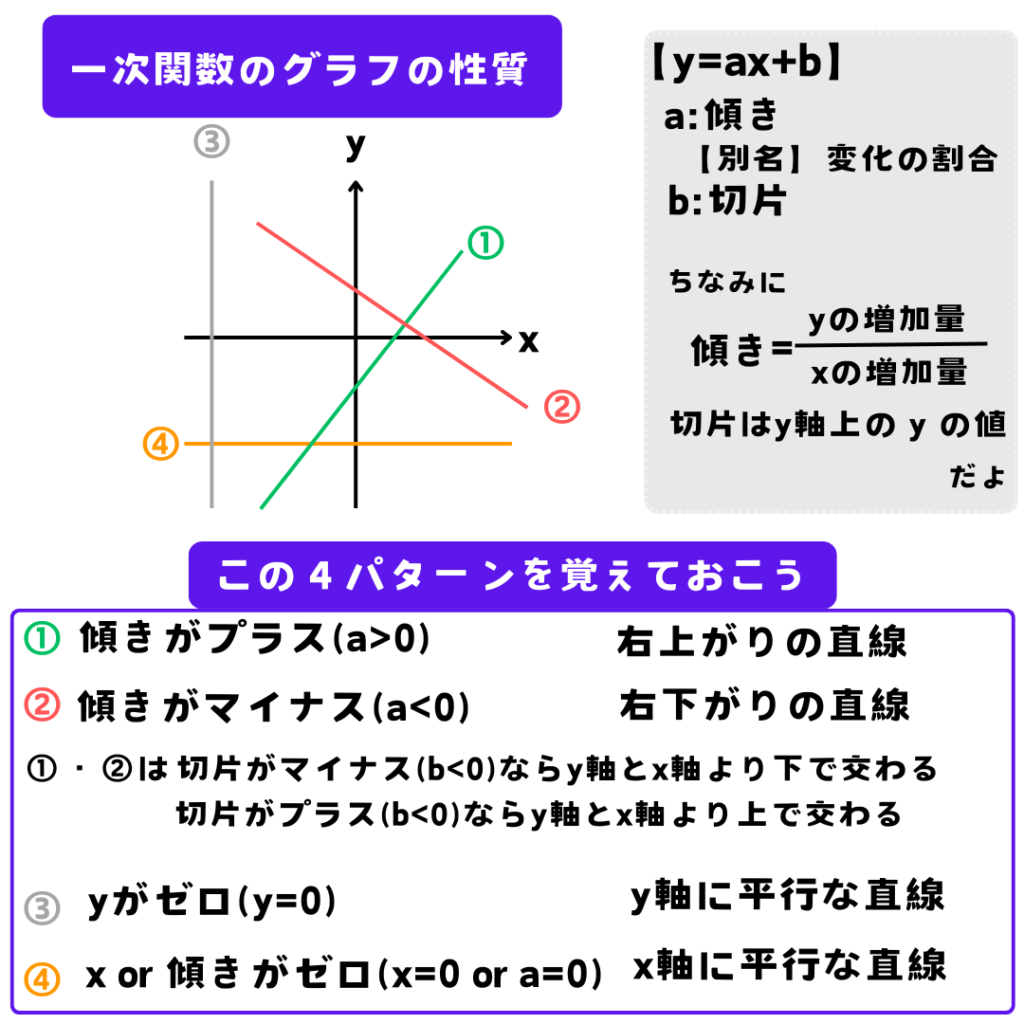
・・・・・・・・・。ありがとうございます。
問題のグラフは右下がりだから傾きはマイナス(負の数)で、切片はx軸の上にあるからプラス(正の数)ってことかなあ?
あってる?


Correct!その通り!
一次関数はそんな性質があるから覚えておいて損のないものです。
ってか覚えておかないと困るシーンはたくさんあるかもね。
ではYさん。a×bの説明にチャレンジしよう!
よし。やってみる。
★一次関数のグラフの性質でグラフが右下がりなので、傾きであるaは負の数、またy軸との交点のy座標である切片は正の数である。
だからa×bは(負の数)×(正の数)なので負の数になる。
いかがですか?


Well done!すばらしい!
はい。Yさんに拍手をお送りください!
負の数・正の数をあらわすときに不等号つかってもよいけど、自信なかったら全然、言葉でかけば問題なし。好きなもの・自分の使いたいものを使おう!
今日は長かったね。もうやさしさも充電切れ、活動限界です。
復活したらまたお会いしましょう!
Take care,Bye!








