【青木島校】3学期期末テストの解き方:中2数学
三角形の証明の解き方
【3学期期末テスト予想問題】

今回は、中2数学の最大の山場、証明について考えていきましょう!
では、問題をズドン!
【問題】
線分ABと線分CDが点Oで交わっているとき、
AB//BD、AO=BOならば、CO=DOであることを証明します。
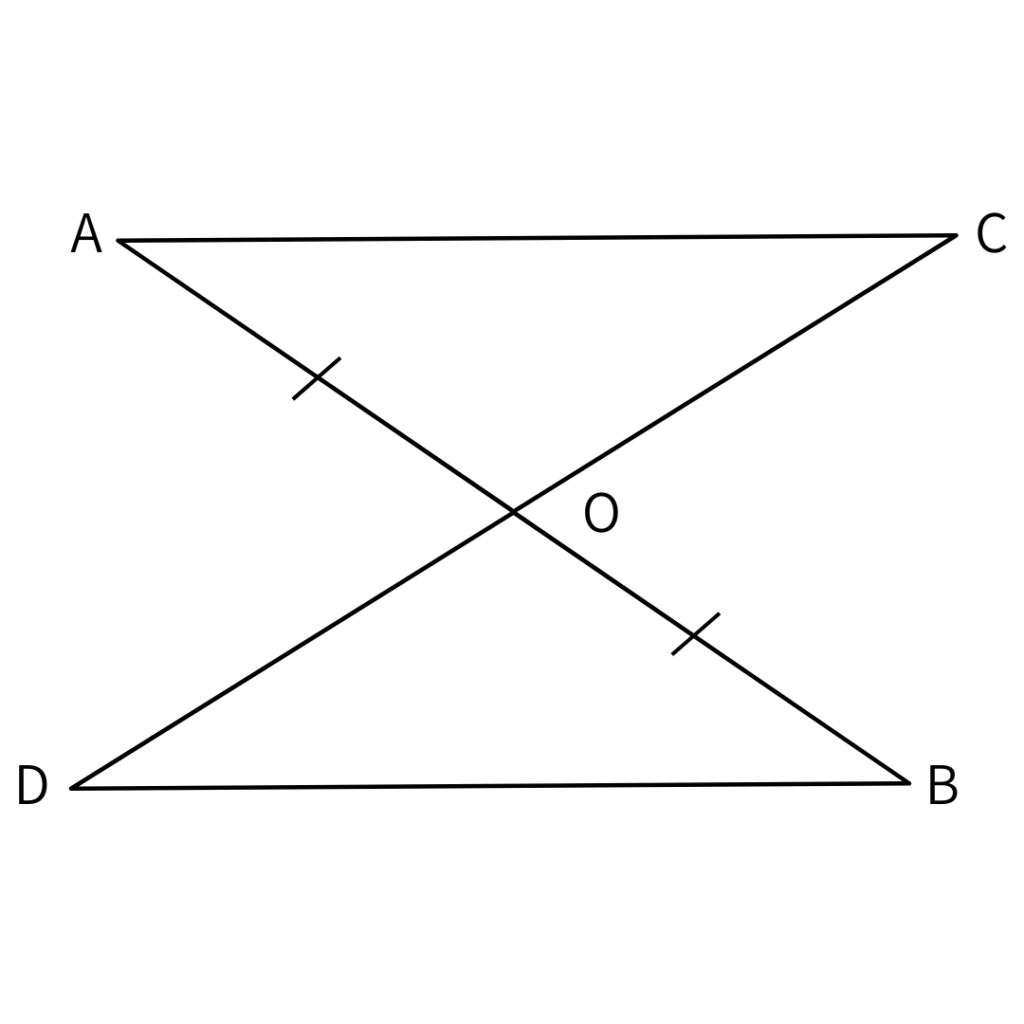
このとき、証明のすじ道は次のようになります。
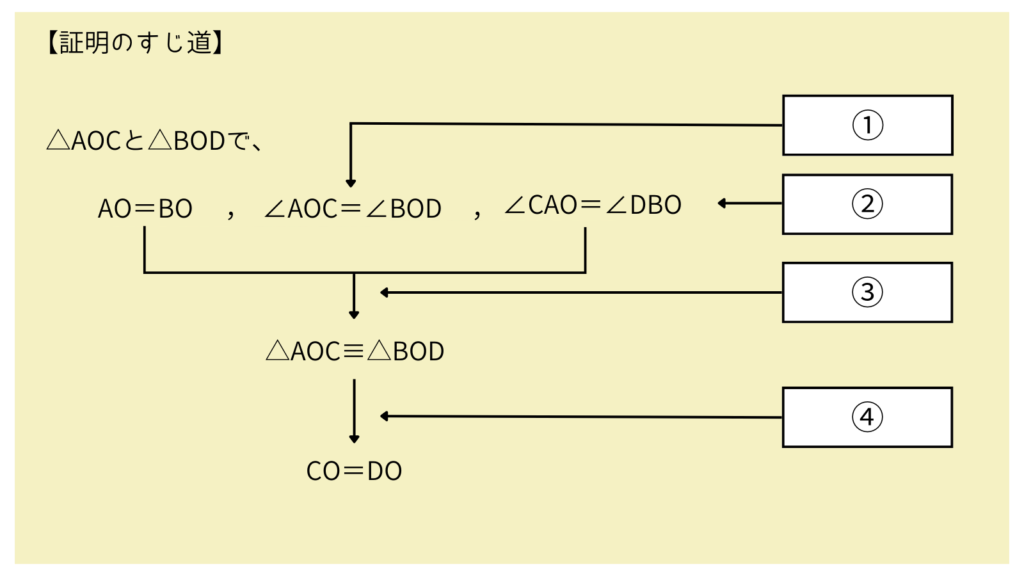
①~④にあてはまる根拠となることがらを
次のア~エから選び、記号を書きなさい。
ア 対頂角の性質 イ 合同な図形の性質
ウ 平行線の錯角の性質 エ 三角形の合同条件
出たね!
ちょうど今学校でやってるけど。
意味がわからない…
なんなんだろうね。
証明って………
証明って……
証明って…
AIに聞いたら
数学における証明とは、ある命題が真であることを論理的に示す過程のこと
だって。
うーん。みかげ先生、助けてもらっていい?


OK!まかしとき!
証明とは…
ある「考え」や「主張(命題)」が本当に正しいことを、「論理的に説明する」こと。
もう少しやさしくすると
【仮定】や数学的に正しいとされている【定理】や【性質】を使って【結論】が正しいがどうかを説明することだね。
(【仮定】は正しいものとするよ。)
うーん。
すこしよくなった気もする。
でもどうやって説明してくのかが謎…。


証明は突然書き出そうとしてもしょせん無理ゲー。
証明のすじ道から考えるようにしよう。
三角形の合同の証明の雛形みたいなものだね。
今回は、その証明のすじ道の考え方を確認していきます。
では、最初に【仮定】と【結論】を考えよう!
【仮定】と【結論】……………
【仮定】と【結論】………
【仮定】と【結論】…


どっかにいっちゃったね…。ふうちさん。
では、一緒に考えよう!
問題によって分かりにくい場合も…。
ただ、今回はとても分かりやすいです。
△△△ならば〇〇〇という文に注目しましょう。
えーっと…
「AC ∥ BD、AO=BOならばCO=DO」
というところのこと?


グッジョブ!
問題文に「ならば」があるときは
【「ならば」の前】が【仮定】
【「ならば」の後ろ】が【結論】だね。
なるほどですね。
なら、
今回は仮定が「AC // BD,AO=BO」
結論が「CO=DO」です!
あってる?


Exactly!
STEP1はクリアかな。
【仮定と結論】はわかった。
うーん…。
ただ、仮定の「AC //BD」の使い方がわかりません。
平行なんて三角形の合同条件になかった気がする…。


ならば、平行線の性質を確認しよう!

だから、仮定の「AC //BD」からは、錯角と同位角が等しくなることがわかる。
なるほど!
そういう使用方法ね。
取扱説明書もしっかり読まないと誤使用しちゃうから、気をつけて。
そういえば…
錯角、同位角、あと対頂角ってのがあったよね。
対頂角はどんなときでも等しい的なやつ。
いま角の関係見てて思い出した。


よし!よきところまで確認できたね。
では、今回の問題の証明のすじ道をもう一度見てみましょう。

はじめに、①と②からだね。
さっき確認した通り、「AO=BO」の根拠は仮定です。
では、①に当てはまる「∠AOC=∠BOD」の根拠となることがらはなに?
選択肢から一つ選んでみよう!
式の形からこれは角っぽい…
∠AOCと∠BODの関係を見ると、
2つの直線が交わってできる向かい合った角だから…対頂角だ!
だから、答えはアです。


すばらしい!
さっき確認したことを上手に使えていますね。
では、②はどうなるの?
はい。
「∠CAO=∠DBO」だから、これも角だ。
ということだよね。
では、答えはウだね。
さっき平行線の性質を確認したから分かりました!


正解です。
仮定の「AC //BD」から平行線の性質が成り立つので、錯角が等しいことを導くことが出来ますね。
平行線の性質はよく使うので、忘れないようにしたいですね!
では、残りの問題を考えてみましょう。
はい!
③は3つの式がまとまってわかることだから…。
よし!それなら、答えはエです。


正解です!
ちなみに、使う三角形の合同条件は答えられるかな?
えーっと…
3つの条件を図に書きこんでみてっと…
おおー!分かりました。
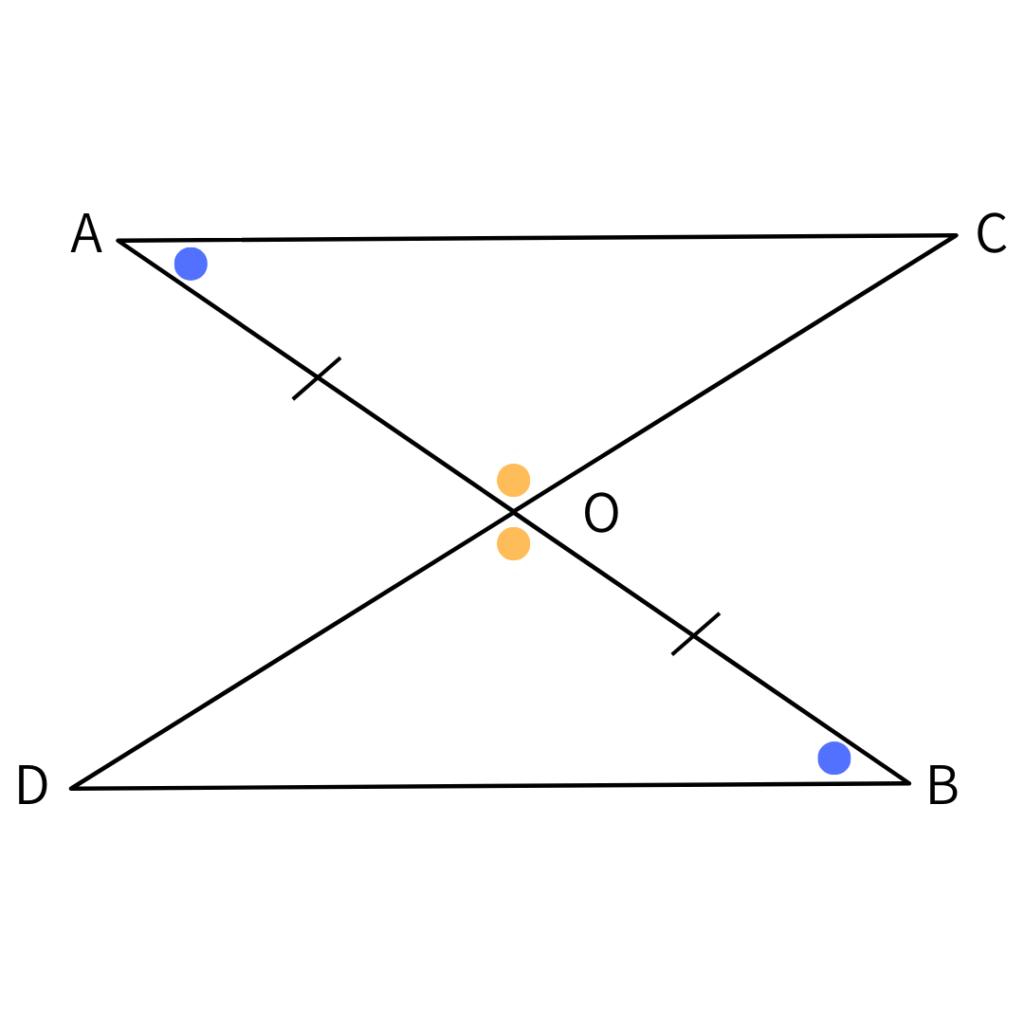
「1組の辺とその両端の角が、それぞれ等しいとき」
ですね!


すばらしい!
図に書きこんでみたところがとてもいいね。
証明を考えるとき、利用できることがらを目で見て確認できるようしておくこと。
これはとても大切です!
お年玉くらいの大切さです!
えっ?めっちゃ大事じゃん!
あとは残ってるのが④の答えだね
だから、最後の④の答えはイです。
うーん。
ただ、この合同な図形の性質って何?


では、確認しておきますか。
結論が辺や角が等しいことである場合には、合同な図形の性質を根拠として使うことが多いよ。

三角形の合同条件も一緒に確認しておこう!
はぁー。
三角形の合同を証明して終わりじゃないのね。
最後までしっかり問題見ないとだね!


おっしゃる通り。
だから、証明のゴールつまり結論を最初によく確認しておくこと。
証明は、ゴール【結論】を決めないでスタートしてもたどりつかないよ。
ゴール【結論】につくために方法を考えて整理し、仮定や仮定から導かれることがらと
あわせて結びつけることがポイントです。
そのためにふうちさんが使った図に整理するということはとてもいい方法です。
OK!みかげ先生。
なんとなくできそうな気がしてきました。


そう!その気持ちが大事!
そして、今しておく最も大切なことは、いろいろな問題を解いて経験を積んでおくこと。
じゃあ、ふうちさんには次にこの問題を解いてもらおうかな!
わーっ…。
もう次があるんですね…
でも、ひとりだとどんな問題を解けばいいか分からない…
だから良かったかな!


そうだね!
証明マスターを目指して一緒に頑張りましょう!
自分一人だとなかなか取り組めない…。
どんな問題が効果的か分からない…。
そんなときはITTO長野に気軽に知らせてね。
精一杯のサポートのお約束をするよ!
お問い合わせはこちらから。
お待ちしております。








