【篠ノ井校】3学期期末テストの解き方:中2数学
等積変形の解き方
【3学期期末予想問題】

今回は等積変形の問題だね。
等積変形とは?
【図形の面積が変わらないように形を変える操作】のこと。
例えば、三角形の形が違っても面積等しいものってあるよね。
それを見つける問題。
今日の問題はこちら!
【問題】
平行四辺形ABCDで、辺CDの中点をMとするとき、△ADMと面積が等しい三角形を3つ答えなさい。
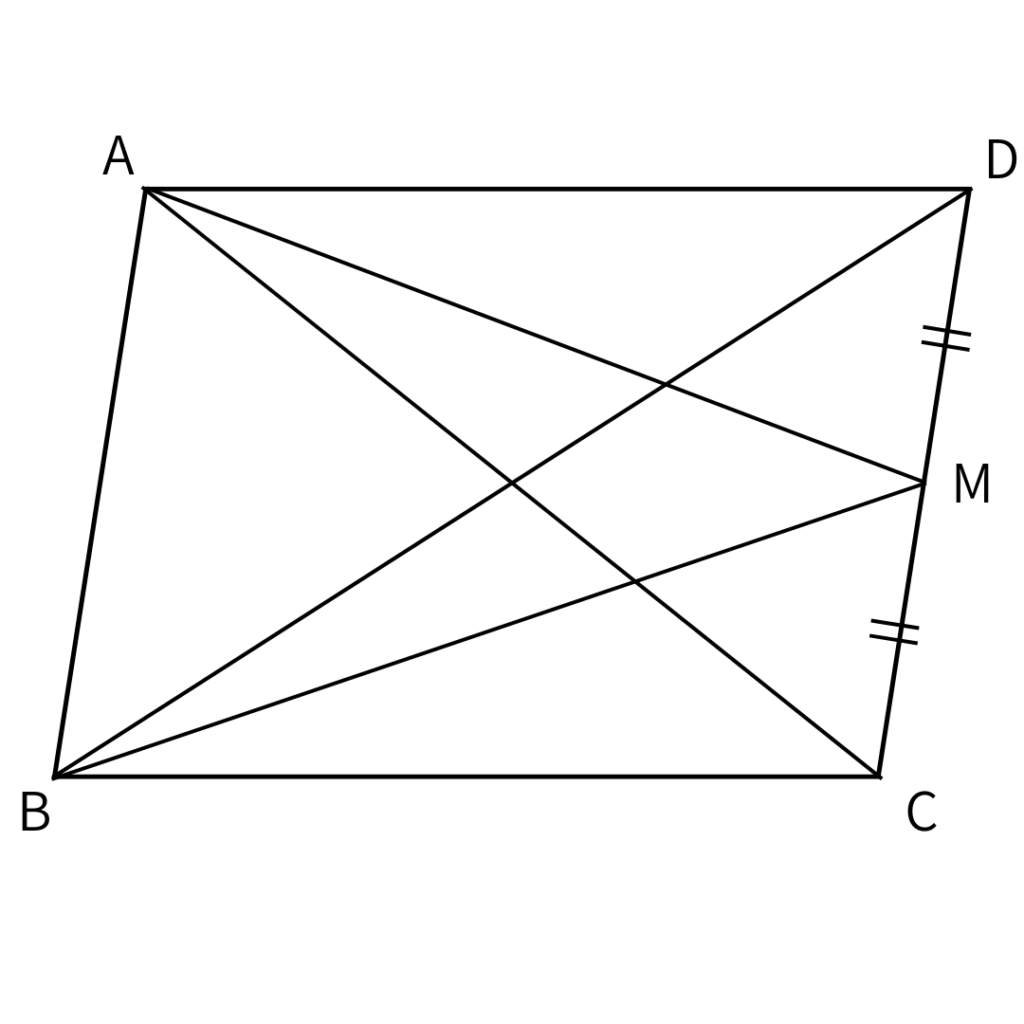
三角形の面積の問題だよね。
三角形の面積って言ったら公式しか出てこない…
\[三角形の面積=\dfrac{1}{2}×底辺×高さ\]だね。
でも図には辺の長さが一つも入っていないよ…
どうするのさ、あやらteacher!


さくらのさん。いいとこに着目できますね!
公式から、三角形の面積ってのは底辺と高さで決まるんだね。
つまり、底辺と高さが同じならすべて面積の等しい三角形になるわけ!
OK! Teacher!
じゃ、△ADMと底辺と高さが同じ三角形をこの図の中から見つけたらいいわけだよね!
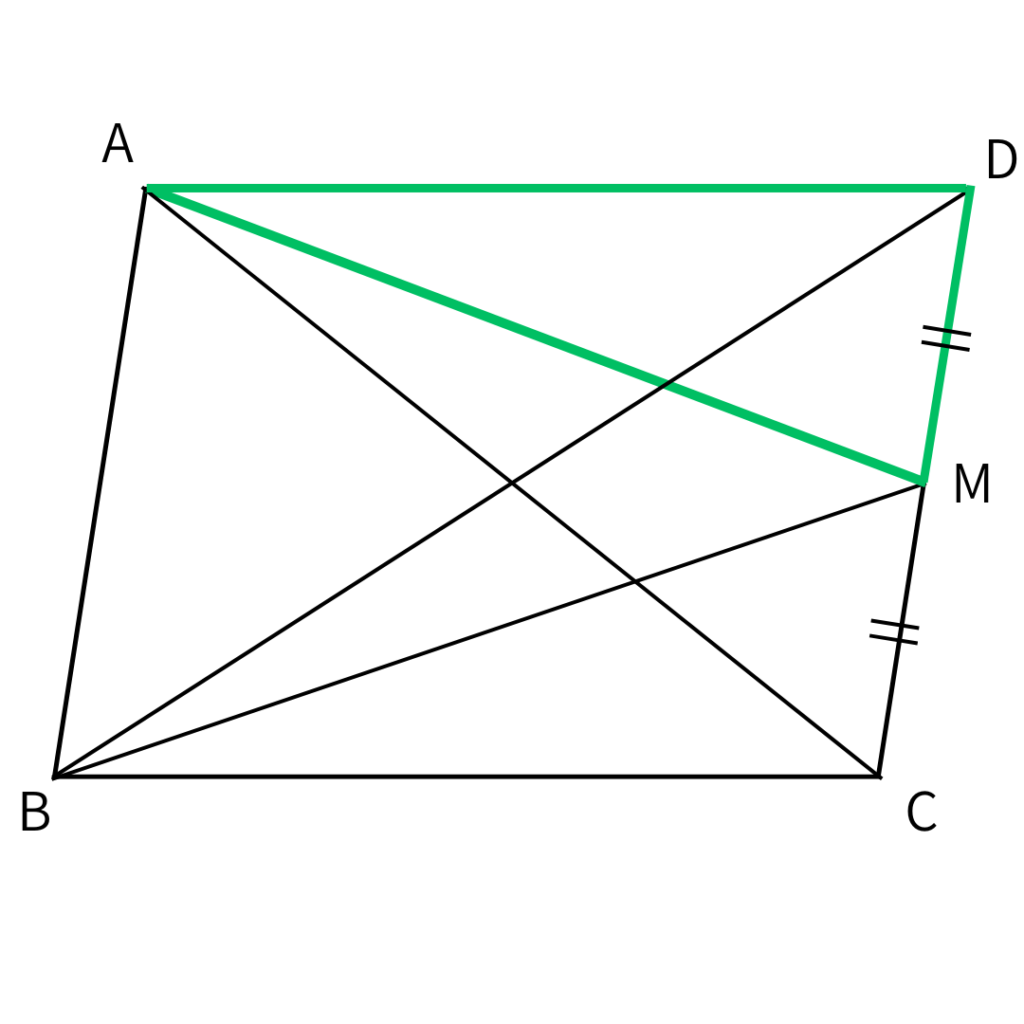
うーん。
さっきも言ったけど図には辺の長さが一つも入っていないよ…
どうしたらいいですか?


いくつかポイントがあるよ!
まず1つ目のポイント。
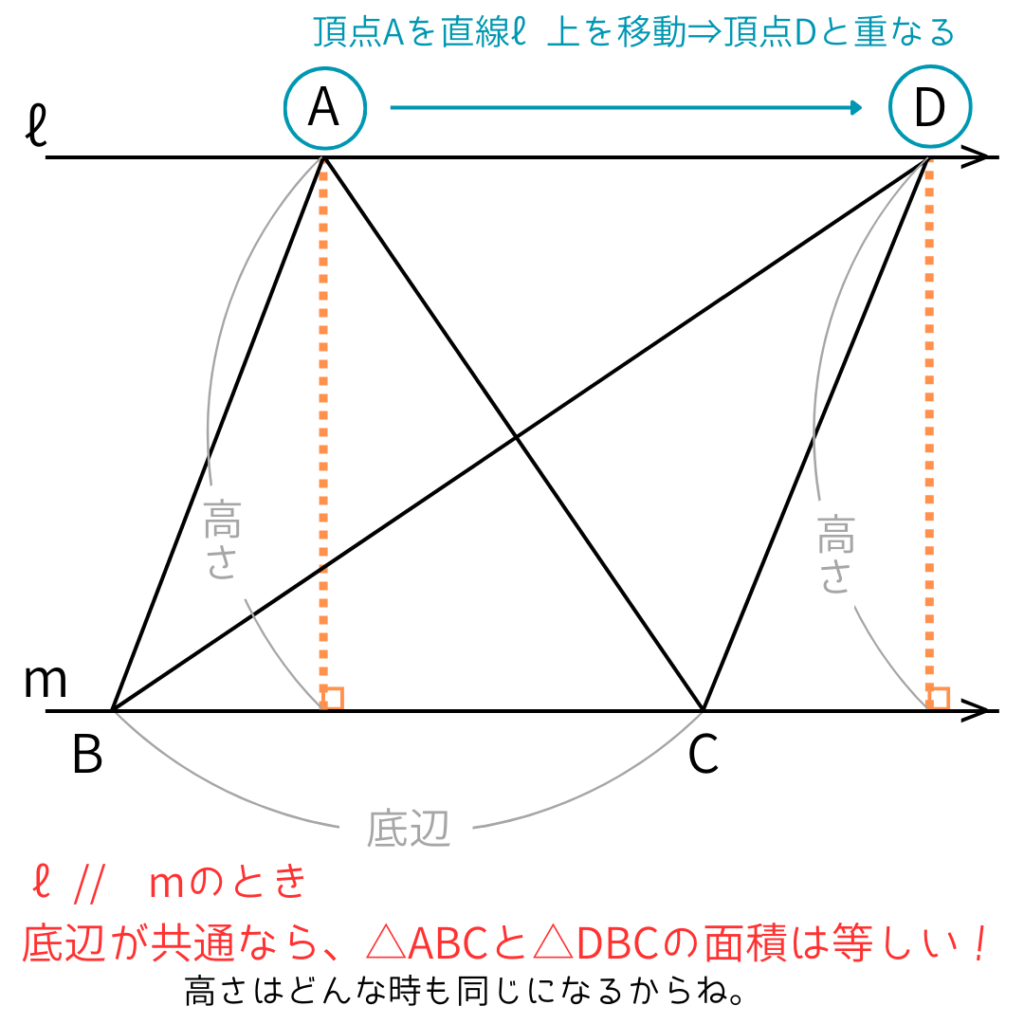
このように
①底辺が共通(同じ)
②底辺と平行な直線上に頂点がある。
⇒高さが等しくなる
①と②両方なら面積も等しくなるってこと!
さくらのさん。
こんな感じの三角形を見つけてみよう!
はいはーい!
じゃ、△ADMと底辺が同じで、底辺と平行な直線上に頂点があるものっと。
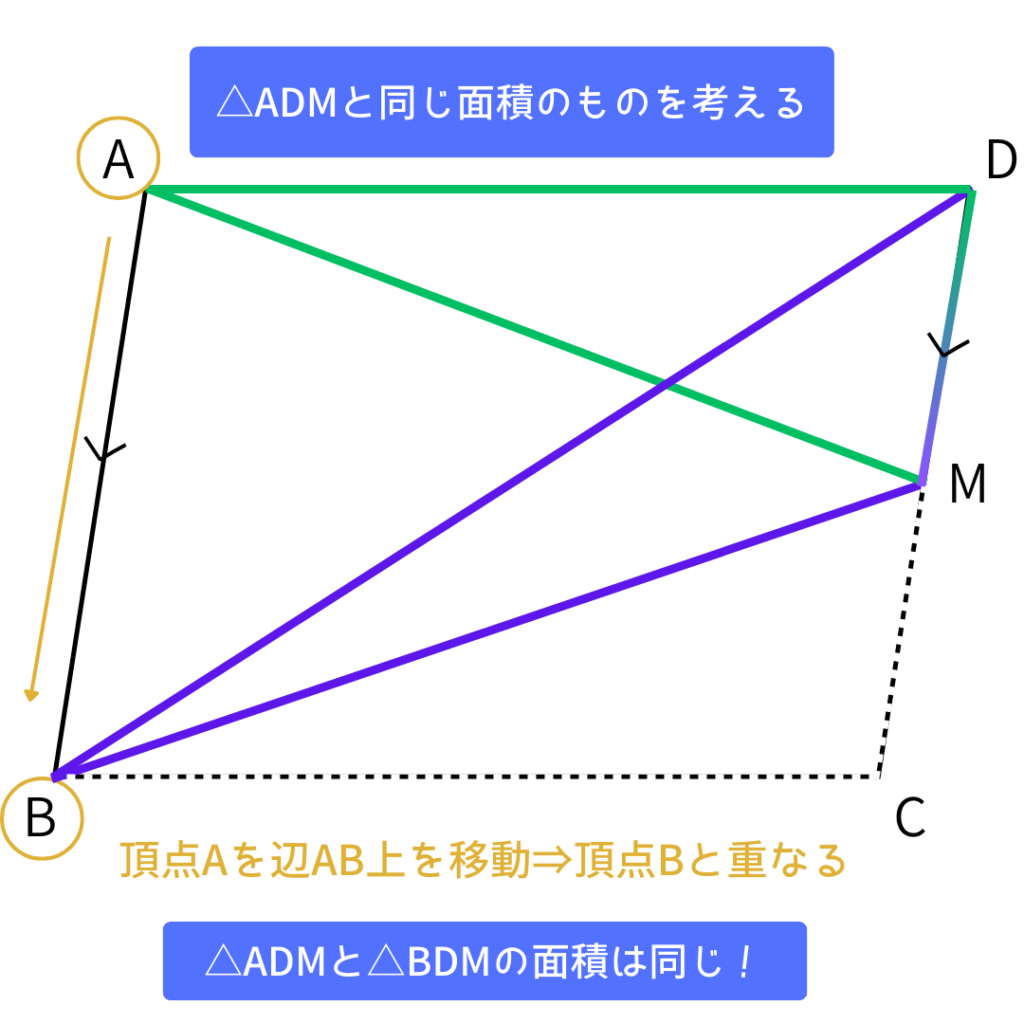
あ!△BDMがそうなってる。
面積が同じ図形は、底辺に平行な線上を
スライドさせるとぴったり重なる三角形に変形できるんじゃない?


正解!その通り!
いい感じだね。
底辺に平行な線上で頂点をスライドさせるとぴったり重なる三角形。
⇒面積が同じ三角形になってる!
これを一つ知ってると見つけやすいかもね。
じゃ、ほかにも探してみよう!
うーん。
あれ?もうない…

じゃ、底辺を辺DAにしてみよう。
すると△ADCと△ADBは底辺DAが共通だけど、明らかに△ADMとは高さが違う…
あ、四角形ABCDは平行四辺形だから…対辺CBの長さも同じはず…
そうすると…
辺BCが底辺なのは、△ABCと△BCDと△BCMかな。
△ABCと△BCDは明らか高さが違う…
△BCMはこれはなんか同じっぽいけど…
ほんとにそうかなあ?
そうなると、一緒のものってないじゃん。


いいところに目がついたね!さくらのさん。
△BCMについてはあとで考えるからちょっと放置しておくよ。
ここで、2つ目のポイント。
【1つの三角形を頂点を通る直線で2つの三角形に分けたとき、底辺の中点を通っていると2つの三角形の面積は等しくなる!】
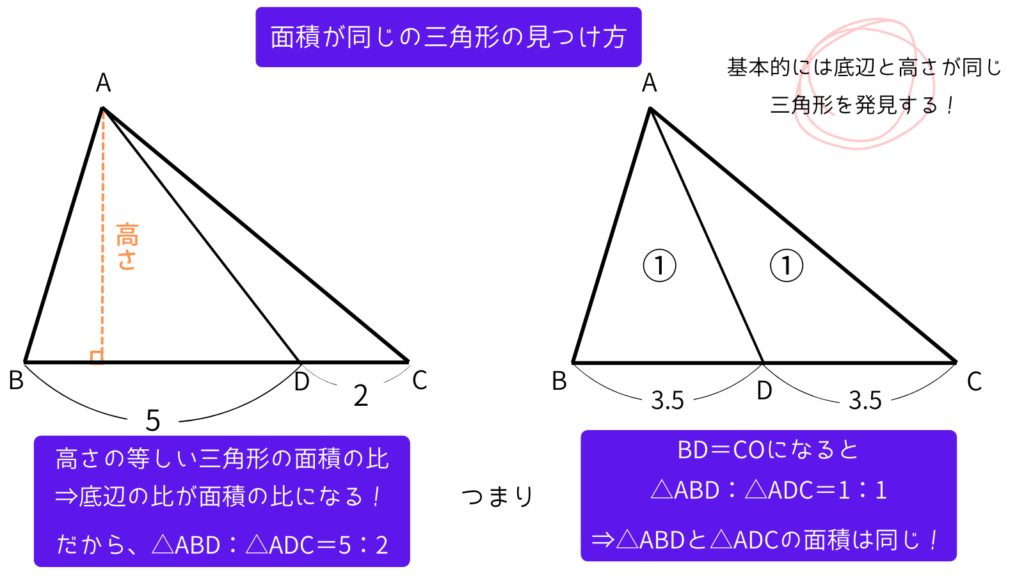
基本的な考え方は同じ。
高さが一緒だから底辺の長さが同じなら面積は同じになるよ。
この面積の比の考え方は、大事な部分だから覚えておいた方が良いよ!
3年生になったら使う頻度は増えるはず。
えーと…
さっきは△ADMの底辺DAを底辺でみたよね。
じゃあ辺DMを底辺で見てみよっと。
おっ!Mは中点だからDM=CMじゃん。
しかも…
△ACDを△ACMと△ADMの2つに分けてる!
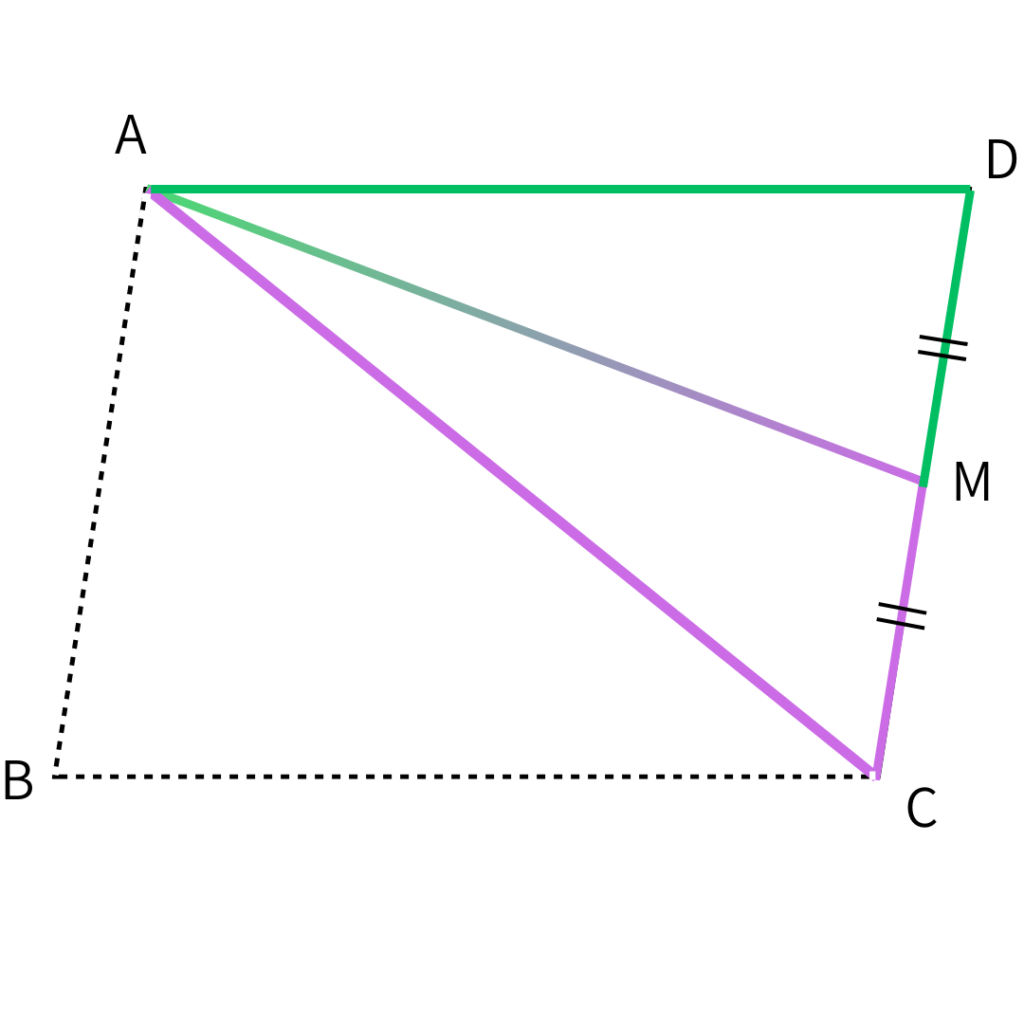
うん。
△ACMは△ADMと同じ面積だよね。


Excellent!
ここで、さっき放置した△BCMについて考えてみよう。
この△BCMと同じ面積の三角形を探してみよう!
ヒントは1つ目のポイントだよ。
1つ目のポイントは、
【底辺が共通】で【高さが同じ】だったよね。
さっきは底辺CBで考えてなかった。
だから、今度は底辺CMで考えよっと。
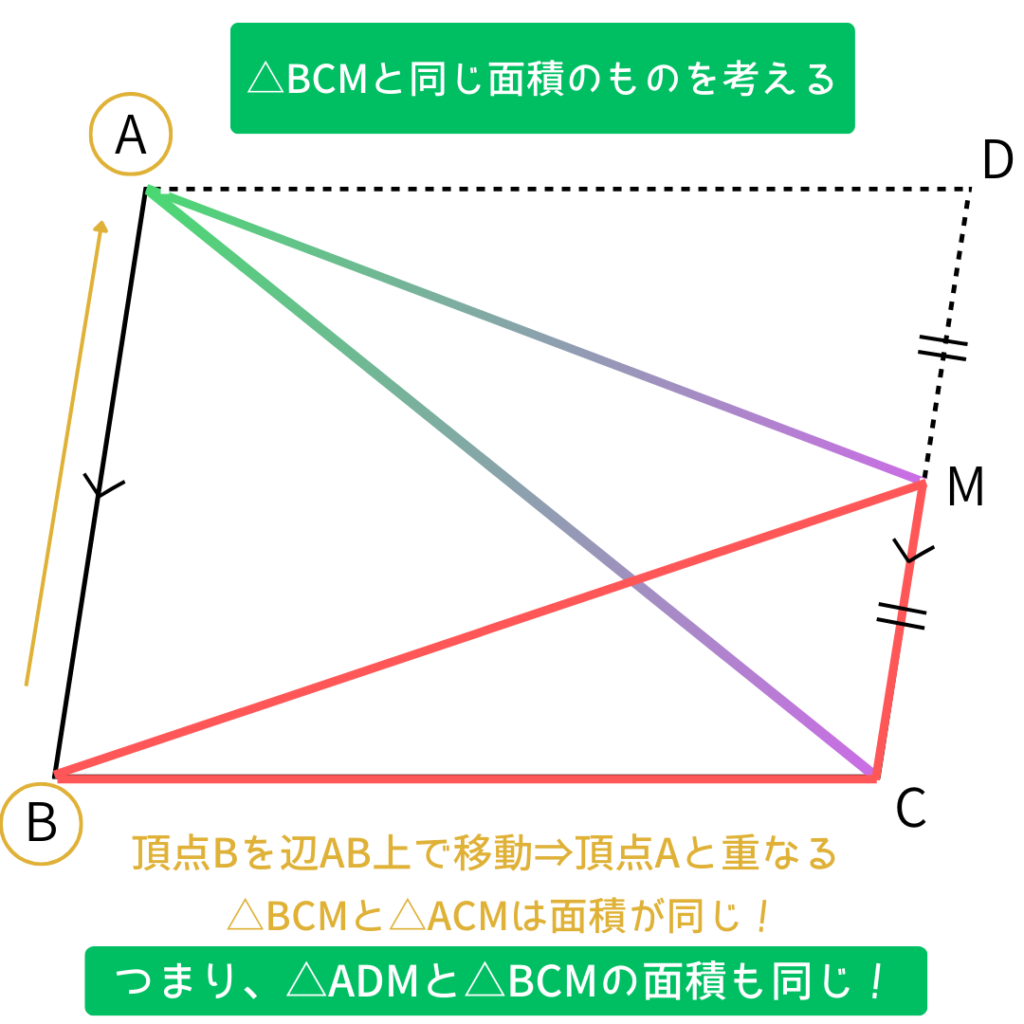
うん。
△ACMは△BCMと同じ面積だよね。
さっき、△ADMと△ACMはいっしょだってやった。
つまりさ…
△ADMと△BCMの面積も一緒じゃん!
なんとなく同じかなって思ったのは当たってたんだね。


You’re right!さくらのさん!
ただ、しっかりとした根拠はあった方がいいからさ。
最後に、3つ目のポイント!
【もとの三角形と同じ面積の変形させた三角形と
同じ面積の三角形を探す。】
だいたい、これで解けない問題はないはず。
△BDM・△ACM・△BCMの3つが答えだね。
Thank you!
あやらTeacher!
なかなか1人だとポイントが整理できないから
一緒にやっていくとわかるところも多くなるよ!
ITTO長野の授業を体験してみよう!(無料だよ)
【わかる!】体験はこちらから!
ギモンに思ったら気軽に知らせてください。
お問い合わせはこちら!
1人だといやになるけど、2人なら大丈夫!
一緒にゴールまで走ろう!








