中学校1年生数学-近似値
単元：近似値
早速ですが、問題です。
2.65が四捨五入によって得られた近似値であるとき真の値aの範囲を不等式をつかって表しなさい。
2.65が四捨五入によって得られた近似値であるとき真の値aの範囲を不等式をつかって表しなさい。
小数第3位を四捨五入して2.65になる一番小さい数字は2.645です。
一番大きいのは2.654ですね。
だから範囲は2.645以上2.654以下です。
不等式にすると2.645≦a≦2.654でいいのかなあ。
一番大きいのは2.654ですね。
だから範囲は2.645以上2.654以下です。
不等式にすると2.645≦a≦2.654でいいのかなあ。
考え方はOKです。
但し2.654以下の表示のところをよく考えてみましょう。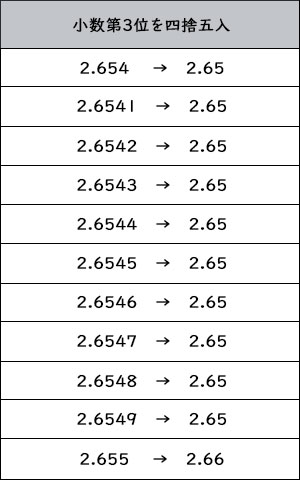
2.654よりもわずかに大きい2.6541～2.6549の小数第３位を四捨五入すると2.65になりますね。
但し2.654以下の表示のところをよく考えてみましょう。
2.654よりもわずかに大きい2.6541～2.6549の小数第３位を四捨五入すると2.65になりますね。
なるほど。
2.6541～2.6549まではすべて該当することになるのですね。
そうすると2.654以下という表示が使えないことがわかりますね。
2.6541～2.6549まではすべて該当することになるのですね。
そうすると2.654以下という表示が使えないことがわかりますね。
ということは2.655を含まない2.655未満にすればよいのですか？
その通りです。
わかった！
表示は2.645≦a＜2.655とすればいいのですか？
表示は2.645≦a＜2.655とすればいいのですか？
正解です。
真の値は2.645≦a＜2.655が正解となります。
ポイントは以上、未満の表示することと小数末尾の数字を５で調整することです。
真の値は2.645≦a＜2.655が正解となります。
ポイントは以上、未満の表示することと小数末尾の数字を５で調整することです。
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。