中学校2年生数学-1次関数（グラフと図形）
単元：1次関数（グラフと図形）の解き方
今日は1次関数のグラフの問題を解いていくよ。
問題
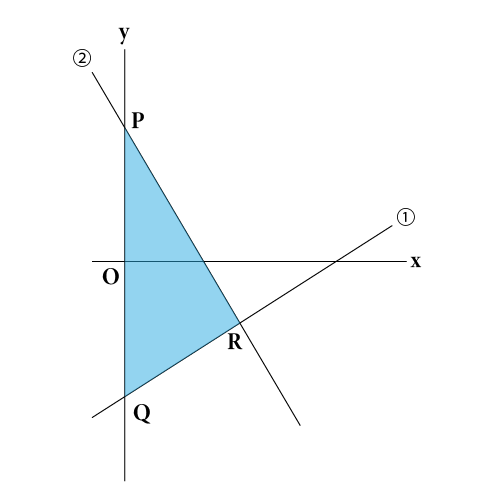
（1）はわかりました！
点Rは直線①と②の交点なので、交点の座標は、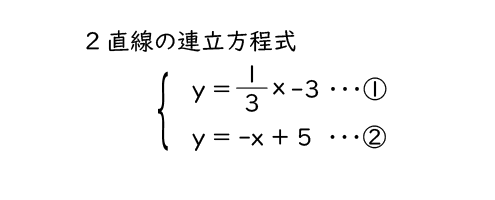
の解と等しくなります。この連立方程式を計算すると、
x ＝ 6、y ＝ -1となるので、点Rの座標は、（6、－1）です。
点Rは直線①と②の交点なので、交点の座標は、
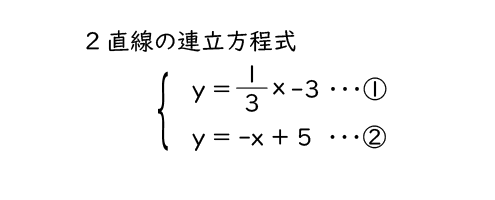の解と等しくなります。この連立方程式を計算すると、x ＝ 6、y ＝ -1となるので、点Rの座標は、（6、－1）です。
すばらしい！
交点の座標は、連立方程式の解で求められるのがポイントですね。
ちなみに、この連立方程式は、代入法で解いた方が計算しやすいですよ。
計算の仕方は次のようになりますので、確認してみて下さい。
では、（2）についても考えてみましょう。
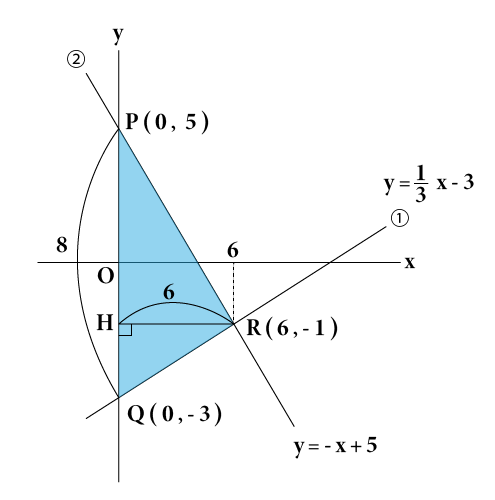
次の図のように，△PQRの辺PQを底辺，点RからPQに垂直に下ろした線分RHを、高さとして考えるとよさそうです。
まず直線①の切片は—3、直線②の切片は5なので、Pの座標は(0，5)、Qの座標は(0，－3)となります。
そうするとOP＝5、OQ=3となるのでPQ＝OP＋OQ＝5＋3＝8、
またRHの長さは点Cのx座標と等しいのでRH＝6、
よって△PQRの面積は8×6÷2＝24です。
正解です！
三角形の辺の長さや高さは、頂点の座標をもとに考えるのがポイントです。
では最後の（3）の問題を考えてみましょう。
三角形の辺の長さや高さは、頂点の座標をもとに考えるのがポイントです。
では最後の（3）の問題を考えてみましょう。
うーん。
（3）はちょっと難しいなぁ…。
（3）はちょっと難しいなぁ…。
ではヒントを出しましょう。
（3）では次のことを使っていくよ。
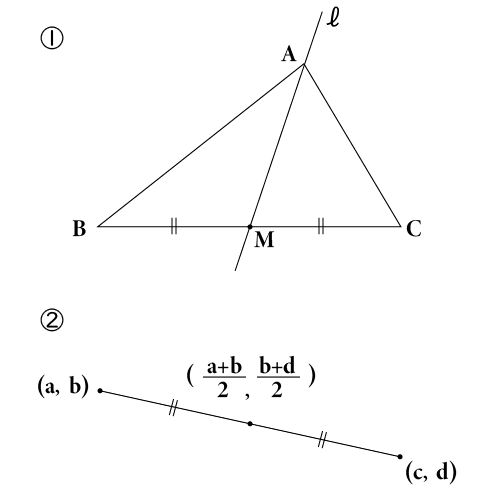
（3）では次のことを使っていくよ。
なるほど！
ということは、点Qを通り△PQRの面積を二等分する直線をℓとすると、直線ℓは次の図のように辺PRの中点Mを通りますね。
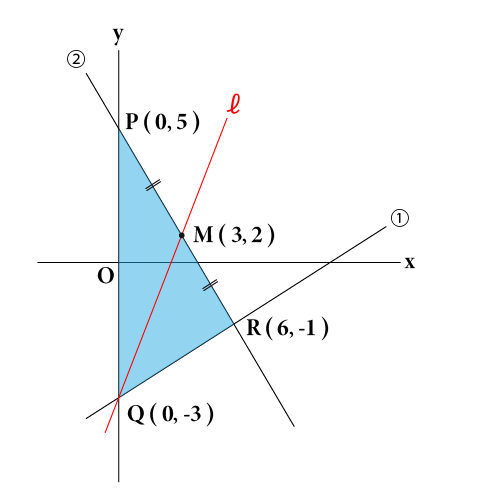
ということは、点Qを通り△PQRの面積を二等分する直線をℓとすると、直線ℓは次の図のように辺PRの中点Mを通りますね。
正解です！
このようなグラフの問題は、長野県のテストや高校入試でもよく出題されるので、たくさん練習しましょう。
このようなグラフの問題は、長野県のテストや高校入試でもよく出題されるので、たくさん練習しましょう。
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。