中学校2年生数学ｰ1次関数の利用（速さ）
単元：1次関数の利用（速さ）
早速問題です！
Aは家を出発して1500ｍ先の店で何分か買い物してから、駅に向かい、出発してから50分後に駅に着いた。
Bは駅をAが出発した同時刻に出発してAが買い物を終え店を出るときにすれ違い、出発してから50分後に家に着いた。
下図は、その時の様子を示す関数グラフである。（いずれも徒歩とする）
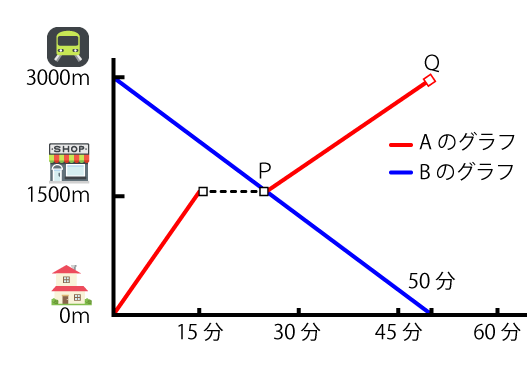
(１)Aが店で買い物をした時間は何分ですか。
(２)Aが店から駅までの歩いた速さは分速何ｍか。
Aは家を出発して1500ｍ先の店で何分か買い物してから、駅に向かい、出発してから50分後に駅に着いた。
Bは駅をAが出発した同時刻に出発してAが買い物を終え店を出るときにすれ違い、出発してから50分後に家に着いた。
下図は、その時の様子を示す関数グラフである。（いずれも徒歩とする）
(１)Aが店で買い物をした時間は何分ですか。
(２)Aが店から駅までの歩いた速さは分速何ｍか。
(１)は、Aが何分買い物をしたかわからないので、買い物した時間をt分としてみます。
いいですね！
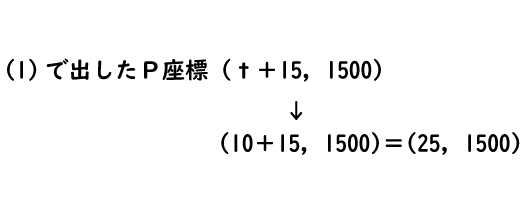
そうすると、買い物を終えたPのx座標はどう考えればよいかな。
そうすると、買い物を終えたPのx座標はどう考えればよいかな。
グラフのP点だから、（15＋ｔ，1500）かな？
OKです。
その次は、BのグラフがPを通っているから、Bの式を出してみよう。
そうしたら、tを出せるかも！
そうしたら、tを出せるかも！
良い考え方です。
Bの式は、50分で3000ｍ歩いているから、
傾きは、グラフ上で右下がりだから-60が傾きとして、切片が3000より
ｙ＝-60ｘ＋3000
傾きは、グラフ上で右下がりだから-60が傾きとして、切片が3000より
ｙ＝-60ｘ＋3000
正解です！！
では、Pの座標をBの式に代入してみよう。
では、Pの座標をBの式に代入してみよう。
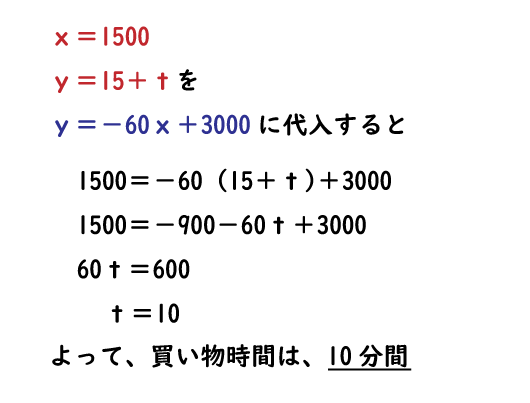
正解！！良く出来ました！
(２)はどうすればいいのかなぁ。
グラフを見ると家から店までの時より遅いような感じだけど。
グラフを見ると家から店までの時より遅いような感じだけど。
良いところに気が付きましたね。
傾きが小さいことは、明らかなので遅いのは確かです。
速さはグラフの傾きと考えることがコツです。
傾きが小さいことは、明らかなので遅いのは確かです。
速さはグラフの傾きと考えることがコツです。
Qの座標は（50，3000）と分かっているから、
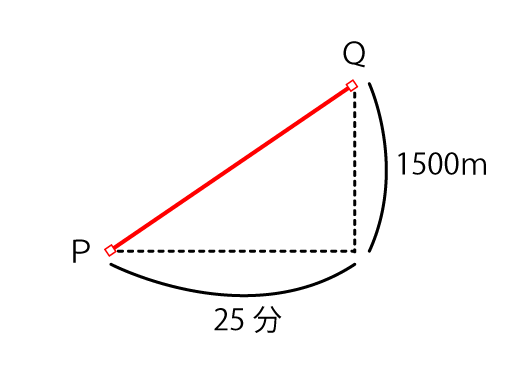
お見事です！
速さは傾きとなっているところがポイントです。
Pの座標を（ｔ＋15，1500）とする所も解くコツですので、よく覚えておきましょう！
速さは傾きとなっているところがポイントです。
Pの座標を（ｔ＋15，1500）とする所も解くコツですので、よく覚えておきましょう！
長野県長野市の中学生数学特訓プラン
各自の実力と志望高、目的に合わせプランはカスタマイズしてご提案しております。詳しくは各教室まで。
基礎力養成特訓プラン
| 推奨学年 | 中学1年～中学3年生 |
| 内容 | 計算の基礎養成演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生：9,130円(税込) |
| 中学2年生：9,570円(税込) | |
| 中学3年生：9,790円(税込) |
発展力養成特訓
| 推奨学年 | 中学1年～中学3年生 |
| 内容 | 文字式・方程式・関数・証明等の文章題読解演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生：9,130円(税込) |
| 中学2年生：9,570円(税込) | |
| 中学3年生：9,790円(税込) |
各種数学特訓プランは以下からお問い合わせ下さい。
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。