【中2】電流の計算(並列回路)
単元:オームの法則(並列回路)の解き方
問題
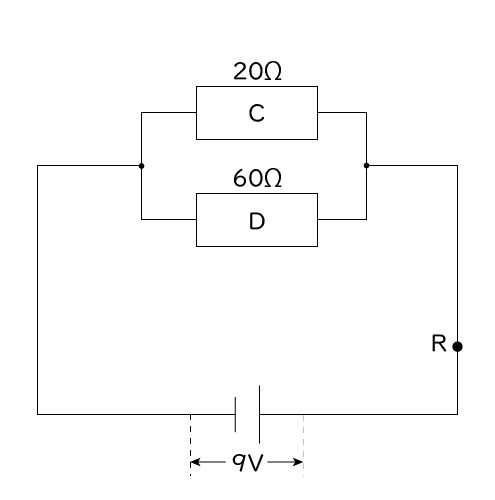
抵抗の大きさが20Ωの電熱線Cと60Ωの電熱線Dを、右の図のように並列につなぎ、電源装置の電圧を9Vにして電圧を加えた。
このとき、次の問いに答えなさい。
(1) 電熱線C、D、点Rに流れる電流はそれぞれ何Aか。
(2) 回路全体の抵抗の大きさは何Ωか。
今日は並列回路の問題を解いていくよ💡
この前学校で直列回路の問題の解き方は習いました💡
並列回路は直列回路と何が違うのでしょうか。
並列回路は直列回路と何が違うのでしょうか。
並列回路では、電流と電圧の大きさの関係が直列回路とは異なるので注意が必要です。次の性質を必ず覚えておきましょう。
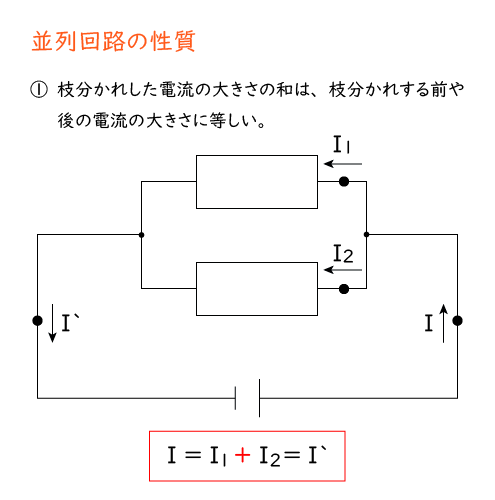
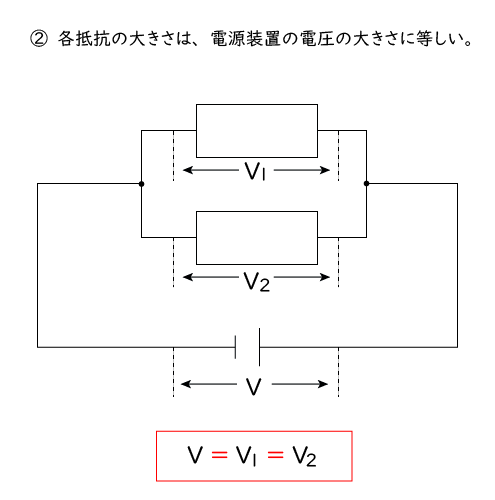
ふむふむ。そうすると、上の②から電熱線C，Dに加わる電圧は，電源装置と同じ9Vということかな?
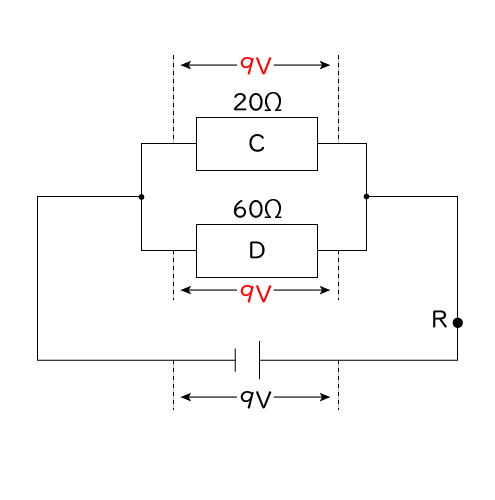
その通りです。それでは次に，各電熱線と点Rに流れる電流の大きさを求めてみましょう。
まず各電熱線の電流の大きさは，各電熱線の抵抗と電圧の値を使って求めます。
その際，オームの法則 ( V(電圧)=R(抵抗)×I(電流) )を使って計算をするのですが，計算方法が分からない時は、下のような図を書いて求めたい部分を隠すとわかりますよ。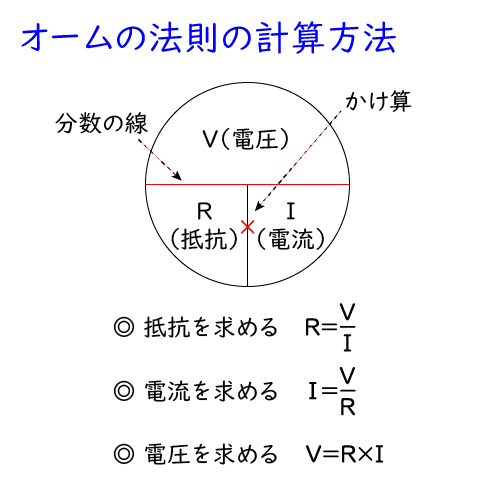
まず各電熱線の電流の大きさは，各電熱線の抵抗と電圧の値を使って求めます。
その際，オームの法則 ( V(電圧)=R(抵抗)×I(電流) )を使って計算をするのですが，計算方法が分からない時は、下のような図を書いて求めたい部分を隠すとわかりますよ。
そうすると電熱線C，Dに流れる電流はそれぞれ、
C：9(V)/20(Ω)＝9÷20=0.45(A)、D：9(V))/60(Ω)=9÷60=0.15(A)、となりますね。
また点Rに流れる電流は，並列回路の性質②から各電熱線に流れる電流の和になるので、0.45+0.15=0.6(A)になります。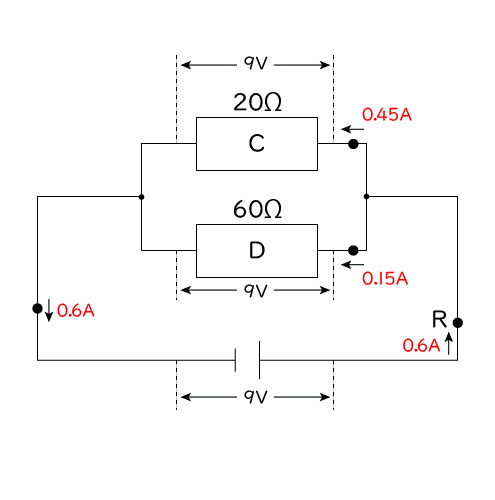
C：9(V)/20(Ω)＝9÷20=0.45(A)、D：9(V))/60(Ω)=9÷60=0.15(A)、となりますね。
また点Rに流れる電流は，並列回路の性質②から各電熱線に流れる電流の和になるので、0.45+0.15=0.6(A)になります。
正解です！では最後に，回路全体の抵抗を求めてみましょう。
回路全体の抵抗は，電源装置に流れる電流と加わる電圧の大きさを使って求めることができます。
回路全体の抵抗は，電源装置に流れる電流と加わる電圧の大きさを使って求めることができます。
えーと，電源装置に流れる電流は0.6A，加わる電圧は9Vなので回路全体の抵抗は9(V)/0.6(A)=9÷0.6=15(Ω)になります。
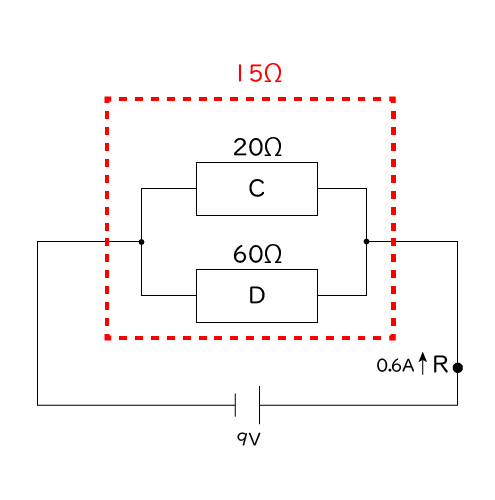
正解です！よくできました。
ここでさらに重要なのは，「並列回路の全体の抵抗は，各抵抗の大きさよりも小さい」という点です💡これはテストでもよく出るので覚えておきましょう。
また，並列回路の全体の抵抗をR，各電熱線の抵抗をR₁，R₂とすると1/R=1/R₁+1/R₂という関係が成り立ちます。これを式変形するとR=(R₁×R₂)/(R₁+R₂)という形になるので，この式を使って全体の抵抗を求めることもできます💡。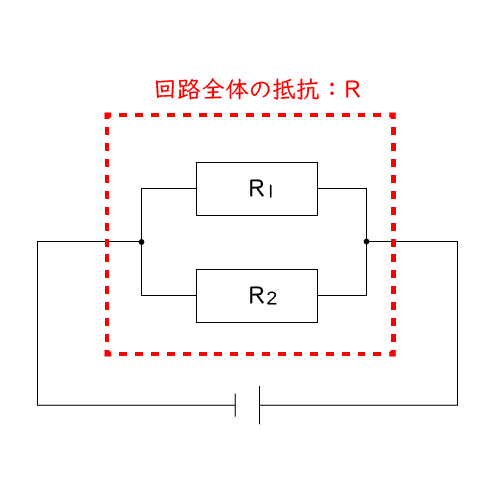
ここでさらに重要なのは，「並列回路の全体の抵抗は，各抵抗の大きさよりも小さい」という点です💡これはテストでもよく出るので覚えておきましょう。
また，並列回路の全体の抵抗をR，各電熱線の抵抗をR₁，R₂とすると1/R=1/R₁+1/R₂という関係が成り立ちます。これを式変形するとR=(R₁×R₂)/(R₁+R₂)という形になるので，この式を使って全体の抵抗を求めることもできます💡。
なるほど💡 分かりました！
ITTO長野の中学生理科プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内いたします。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生理科プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。